Решение проблемы повышения надежности изделий является одной из важнейших задач, имеющих большое народнохозяйственной значение, которое в конечном итоге приводит к экономическому эффекту. Учитывая, что как для восстанавливаемых, так и для невосстанавливаемых, так и для невосстанавливаемых изделий, повышение надежности обеспечивается несколькими способами, то важно выбрать такой способ, при котором получается максимальный экономический эффект.
Как известно, в случае невосстанавливаемого устройства требуемая надежность может быть достигнута при повышении надежности его отдельных элементов конструкторско-производственными способами, или применением общего резервирования, или совместным применением обоих способов.
В данной статье решается задача нахождения оптимального с точки зрения наименьших затрат способа повышения надежности невосстанавливаемых устройств и определения соответствующих ему соотношений между надежностью, стоимостью и количеством резервируемых устройств.
Стоимость невосстанавливаемого устройства при повышении надежности можно определить, исследуя математическую модель стоимости в зависимости от параметра надежности по формуле [2].
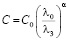 , (1)
, (1)
где С = С (Р0, Р3) – функция стоимости изделия при повышении его надежности от Р0 до Р3; С0 – стоимость изделия с надежностью Р0; λ0 и λ3 – интенсивности отказов, соответствующие значениям надежности Р0 до Р3; α= (0.5÷1.5) – коэффициент, зависящий от уровня разработки и производства.
Стоимость М устройств (Су), необходимых для достижения надежности Р3, требуемой для выполнения определенной задачи, будет равна:
Су = С M, (2)
где М – количество устройств, необходимых для достижения требуемого значения надежности Р3, определяется из формулы общего резервирования.
Р3 = 1 – (1 –Р)М, (3)
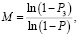
где Р3 – требуемая надежность М устройств; Р – надежность одного устройства.
Если интенсивность отказов λ распределена экспоненциально, то надежность (вероятность безотказной работы) выражается формулой:
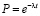 , (4)
, (4)
где t – время безотказной работы.
Из (1), (2), (3), (4) имеем:
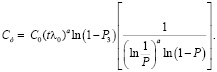 (5)
(5)
Для нахождения выражения оптимального значения надежности Ропт (соответствующего минимальным экономическим затратам), до которого следует повышать надежность одного устройства, продифференцируем уравнение (5) по Р и приравняем производную к нулю:
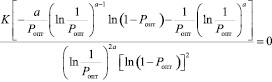 , (6)
, (6)
где K = Со(λоt)a ln(1–Рз).
После несложных преобразований (6) имеем:
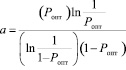 . (7)
. (7)
На рисунке показана зависимость Ропт = f(а).
Обозначим значения коэффициента а, соответствующие начальной надежности устройства Ро и надежности Рз, ао и аз соответственно.
Сравнивая значения коэффициента а со значениями ао и аз, можно решить, какой способ повышения надежности данных невосстанавливаемых устройств до заданного значения Рз будет экономически эффективным, то есть оптимальным с точки зрения получения минимальных затрат.
В случае а ≥ ао, что соответствует Ропт ≤ Ро, необходимое значение надежности Рз можно получить только применением резервных устройств с надежностью Ро, число которых Мо определяется по формуле (3).
Если а ≤ аз, что соответствует Ропт ≥ Ро, следует повышать надежность устройства до Рз без применения резервирования (Мз = 1).
Если аз < а < ао, (Рз > Ропт > Ро), следует повышать надежность одного устройства до Ропт и применять М резервных устройств с надежностью Ропт.
Определив Ропт по формуле (7), вычисляют число резервных устройств М:
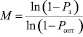 .
.
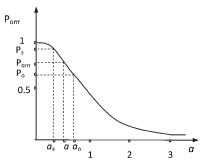
Зависимость оптимальной надежности Ропт одного устройства от коэффициента а
Пример. Для сбора измерительной информации о работе проветривания шахты прибор, необходимый для выполнения измерительных операций над получаемыми от датчиков величинами, должен обладать надежностью Рз = 0,95 в течение t = 10 ч. Предположим, что наиболее подходящий (из имеющихся) прибор обладает всеми необходимыми техническими характеристиками, кроме надежности (Ро= 0.7), и имеет стоимость Со = 10000 руб.
Требуется определить стоимость Су1 , получающуюся при оптимальном способе повышения надежности Ропт , и число резервных приборов М, если а = 0.55.
По формуле (7) определяем: аз = 0.336, ао = 0.692, Ропт = 0.8.
Так как аз < а < ао , то надежность Рз следует обеспечить повышением надежности одного устройства конструкторско-производственными способами до Ропт = 0,8 и резервированием кратностью М. Находим М по формуле (3):
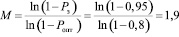 .
.
Выбираем М = 2, из формулы (3) определяем значение надежности Ропт:
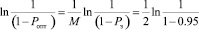 ,
,
Ропт = 0,78.
Далее вычисляем по формуле (4) интенсивности отказов:
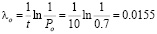 ч–1,
ч–1,
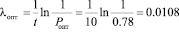 ч–1,
ч–1,
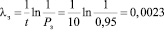 ч–1.
ч–1.
Из выражения (1) и (2) определяем Су1:
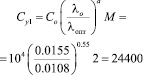 руб.
руб.
Если применить только одно устройство (Мо = 1) с Рз = 0,95, то его стоимость будет:
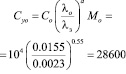 руб.
руб.
Так как Су1 < Суо, то обеспечить оптимальную надежность Р = 0.95 можно путем повышения надежности устройства конструкторско-производственными способами от Ро = 0.7 до Ропт = 0.78 и применением двух устройств (М = 2).
Таким образом, в данной статье рассмотрен метод определения оптимального способа повышения надежности невосстанавливаемых устройств до заданного значения и соответствующих этому способу соотношений между надежностью, стоимостью и количеством резервных устройств.
Библиографическая ссылка
Хачaтрян С.А. ВЫБОР ОПТИМАЛЬНОГО СПОСОБА ПОВЫШЕНИЯ НАДЕЖНОСТИ НЕВОССТАНАВЛИВАЕМЫХ ОБЪЕКТОВ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 12-5. – С. 785-787;URL: https://applied-research.ru/ru/article/view?id=10926 (дата обращения: 27.04.2024).

