Использование системы опознавания «свой-чужой» в низкоорбитальных системах спутниковой связи (ССС) позволяет повысить информационную скрытность данной системы связи. Применение протокола типа «запрос-ответ», основанного на доказательстве с нулевым разглашением данных, позволяет однозначно аутентифицировать космический аппарат (КА). При этом для обеспечения требуемого уровня криптозащиты в данной системе будет использоваться достаточно большой модуль р, который применяется в процессе вычислений. Такая одномодульная структура характеризуется значительными схемными затратами, что приводит к увеличению вероятности возникновения сбоев и отказов в работе системы.
Поэтому придание запросно-ответной системе, используемой для аутентификации КА, свойства отказоустойчивости является актуальной задачей.
Цель исследования. Возрастание требований к технико-экономическим характеристикам современных систем спутниковой связи, а также обеспечение требуемого уровня их имитостойкости привели к необходимости использования запросно-ответных систем, позволяющих определить статус КА. Для обеспечения требуемого уровня имитостойкости таких систем опознавания «свой-чужой» в работах [1,2] предлагается использовать протокол, основанный на доказательстве с нулевым разглашением знаний. Данный протокол обладает достаточно высокой криптостойкостью.
Однако в процессе работы запросно-ответной системы могут возникнуть сбои и отказы, которые приведут к искажению результатов вычислений. Для устранения таких последствий необходимо, чтобы система опознавания обладала свойством устойчивости к отказам. Эффективные результаты можно получить с помощью использования модулярных кодов. В данных кодах вычисления производятся параллельно и по независимым вычислительным каналам. Это свойство модулярных кодов можно использовать при разработке отказоустойчивой системы опознавания статуса КА.
Поэтому целью данной работы является повышение отказоустойчивости запросно-ответной системы, применяемой в низкоорбитальных системах спутниковой связи, на основе использования непозиционных модулярных кодов, которые способны осуществлять поиск и коррекцию ошибок, вызванных сбоями и отказами оборудования.
Материалы и методы исследования
В процессе использования низкоорбитальных систем спутниковой связи широкое внимание уделяется вопросам обеспечения высокой надежности работы бортовых комплексов. Введение в состав космического аппарата системы опознавания «свой-чужой» приводит к увеличению схемных затрат. Поэтому при разработке структуры запросно-ответной системы особое внимание уделяется вопросам обеспечения отказоустойчивости работы такой системы. Так как обеспечение масса-габаритных показателей для оборудования КА является достаточно жестким, то для обеспечения устойчивости к отказам и сбоям, которые могут возникнуть в процессе работы системы опознавания, целесообразно использовать алгебраические системы, обладающие свойством кольца и поля.
Особое место среди таких алгебраических систем занимают модулярные коды. В настоящее время среди непозиционных модулярных кодов можно выделить две большие группы. Основу первой группы составляют непозиционные коды системы остаточных классов (СОК). При построении таких кодов классов вычетов в качестве оснований применяются взаимно простые числа [4, 6, 7]. Благодаря этому любой позиционный код можно представить в виде набора остатков, полученных при делении этого числа на числа-основания:
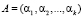 , (1)
, (1)
где 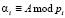 ;
; 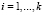 .
.
Основу второй группы непозиционных кодов составляют модулярные полиномиальные коды, в частности, коды полиномиальной системы классов вычетов (ПСКВ) [5, 8]. При построении таких кодов классов вычетов в качестве оснований применяются неприводимые полиномы. Благодаря этому любой позиционный код представляется в самом начале в полиномиальной форме, а затем полученному полиному в соответствие ставится набор остатков, полученных при делении этого числа на модули:
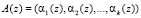 , (2)
, (2)
где 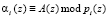 ;
; 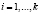 .
.
Несмотря на различия, данные модулярные коды имеют много общего. Данные коды, за счет параллельной и независимой обработки вычетов, позволяют повысить скорость выполнения следующих модульных операций:
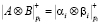 , (3)
, (3)
где 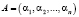 и
и 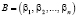 – модулярный код в кольце вычетов;
– модулярный код в кольце вычетов; 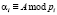 ;
; 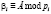 ;
; 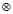 – операции сложения, вычитания и умножения по модулю основания кода СОК pi; i = 1, …, k.
– операции сложения, вычитания и умножения по модулю основания кода СОК pi; i = 1, …, k.
В работах [2, 3] представлен протокол аутентификации космического аппарата, использующий доказательство с нулевым разглашением данных. Данный протокол применяется при определении статуса КА, который попадается в зону видимости станции спутниковой связи, расположенной на необслуживаемом объекте. С целью повышения его эффективности был разработан протокол, использующий модулярные коды.
Для организации процесса работы системы опознавания используется секретный ключ U. При этом открытый ключ спутника, который используется при решении уравнения двойного использования сеансового ключа S(i), определяется
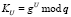 , (4)
, (4)
где q – простое число; g – первообразный элемент, порождающий группу q.
Чтобы выполнить протокол аутентификации КА с помощью модулярных кодов, необходимо выбирать основания р1, …, pk, так, чтобы диапазон Р кода СОК удовлетворял
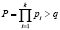 , (5)
, (5)
где pi – простые числа, в которых g – первообразный элемент.
Затем вычисляем значение истинного статуса КА в системе остаточных классов:
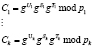 , (6)
, (6)
где 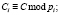
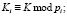
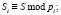
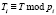 ; С – статус КА; S – параметр, который используется для вычисления сеансового секретного ключа; T – параметр, который используется для обнаружения двойного применения сеансового ключа.
; С – статус КА; S – параметр, который используется для вычисления сеансового секретного ключа; T – параметр, который используется для обнаружения двойного применения сеансового ключа.
Данное значение истинного статуса КА в виде кода СОК (С1, С2, …, CL) заносится в блок памяти ответчика, который располагается на борту спутника. Затем пользователь проводит «зашумление» своих секретных данных. При этом используются случайные значения 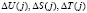 , где j – номер сеанса связи:
, где j – номер сеанса связи:
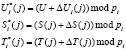 . (7)
. (7)
В результате получаются значения
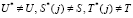 .
.
После этого система вычисляет новый «зашумленный статус КА» согласно
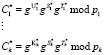 (8)
(8)
где С* – зашумленный статус спутника; 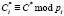 .
.
На следующем этапе запросчик пересылает пользователю число 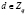 . Ответчик приступает к вычислению ответа на вопрос d.
. Ответчик приступает к вычислению ответа на вопрос d.
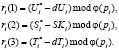 (9)
(9)
Полученные ответы на поставленный вопрос d передаются запросчику. Затем запросчик приступает к проверке доказательства истинности пользователя:
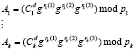 . (10)
. (10)
Если космический аппарат является своим, то справедливо равенство
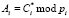 . (11)
. (11)
Представленный выше алгоритм работы запросно-ответной системы в модулярных кодах можно аналогичным образом реализовать с использованием полиномиальной системы классов вычетов. Рассмотрим разработанный алгоритм коррекции ошибок с использованием минимальной избыточности. Для этого в систему оснований 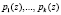 , с рабочим диапазоном
, с рабочим диапазоном
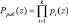 ,
,
введем одно основание pn+1(z), которое удовлетворяет условию
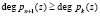 . (12)
. (12)
Тогда в избыточном коде полиномиальной системе классов вычетов полином A(z) представляется как набор остатков
A(z) = (α1(z), α2(z),…, αn(z), αn+1(z)), (13)
где 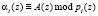 pi(z) – минимальный многочлен, определяемый в расширенном поле Галуа GF (2v).
pi(z) – минимальный многочлен, определяемый в расширенном поле Галуа GF (2v).
Для определения ошибок в коде ПСКВ используется полиномиальная форма позиционной характеристики интервала, которая определяется
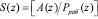 . (14)
. (14)
Используя модульные операции, определим значение интервал-кода:
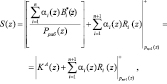 (15)
(15)
где 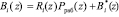 – ортогональный базис полной, состоящей из n+1 оснований, ПСКВ;
– ортогональный базис полной, состоящей из n+1 оснований, ПСКВ; 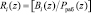 ;
; 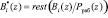 – ортогональный базис системы с основаниями p1(z), p2(z),…, pn(z);
– ортогональный базис системы с основаниями p1(z), p2(z),…, pn(z); 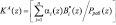 – количество переходов за величину рабочего диапазона Рраб(z).
– количество переходов за величину рабочего диапазона Рраб(z).
Значит, значение KA(z) будет определяться только значениями произведений 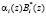 , i=1,…, n. Тогда выражение (15) можно представить в виде
, i=1,…, n. Тогда выражение (15) можно представить в виде
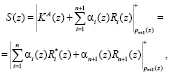 (16)
(16)
где
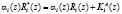 ;
;
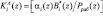 –
–
количество переходов за рабочий диапазон Рраб(z), которое возникнет при значении остатка αi(z); i =1,…, n.
Результаты исследования и их обсуждение
Рассмотрим работу разработанного протокола с использованием кода СОК. Пусть выбраны основания р1 =11, р2 = 13, р3 = 19. Тогда диапазон СОК будет равен Р = 2717. В качестве первообразного элемента данной группы возьмем g = 2. Пусть значение секретного ключа равно U = 3. Пусть значения S = 5 и T = 5. Представим данные параметры в СОК:
K = (3, 3, 3), S = (5, 5, 5), T = (5, 5, 5).
Используем (6) для вычисления представления:
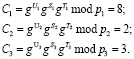
Полученный истинный статус спутника С = (8, 2,3) записывается в память ответчика.
Затем проводится «зашумление» секретных данных. При этом используются значения 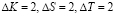 . Тогда зашумленные значения U* = (5, 5, 5), S= (7, 7, 7) и Т=(7, 7, 7).
. Тогда зашумленные значения U* = (5, 5, 5), S= (7, 7, 7) и Т=(7, 7, 7).
После пользователь вычисляет «зашумленное вручение» согласно (8)
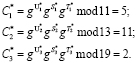
Пусть запросчик пересылает спутнику число 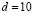 .
.
Ответчик вычисляет ответы на вопрос d = 10. Первый ответ в коде СОК равен
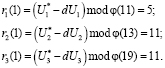
Второй ответ в коде СОК равен
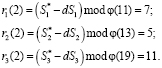
Третий ответ в коде СОК равен
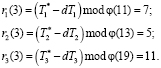
Полученные ответы (5, 11, 11), (7, 5, 11), (7, 5, 11) передаются запросчику, который приступает к проверке доказательства истинности пользователя. Для этого вычисляется
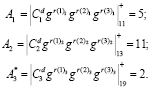
Так как
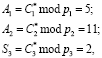
то статус КА «свой» и запросчик разрешает начать сеанс связи.
Рассмотрим разработанный алгоритм коррекции ошибок с помощью модулярного кода. Пусть p1(z)=z+1, p2(z)=z3+z2+1, p3(z)=z3+z+1. В качестве контрольного основания используем p3(z). Тогда
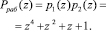
Вычислим ортогональные базисы ПСКВ:
B1(z)=z6+ z5+ z4+ z3+ z2+z+1;
B2(z)=z6+z5+z3+1;
B3(z)=z4+z2+z+1.
Представим ортогональные базисы в виде
B1(z)=R1Pраб(z)+B1*=(z2+z);
Pраб(z)+(z3+z2+1);
B2(z)=R2Pраб(z)+B2*=(z2+z+1);
Pраб(z)+(z3+z2); B3(z)=R3Pраб(z)= 1 Pраб(z).
Получаем систему безызбыточных оснований p1(z)=z+1, p2(z)=z3+z2+1, в которой определены ортогональные базисы
B1*(z)= z3+z2+1,
B2*(z)= z3+z2.
Пусть 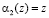 . Вычислим значение
. Вычислим значение 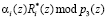 . Тогда получаем
. Тогда получаем
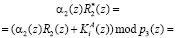
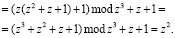
Возьмем полином А(z)= z3+z2+z+1, который принадлежит Pраб(z). В ПСКВ данный полином имеет вид A(z)=(0, z, z2). Определим значение интервала S(z) согласно (16)
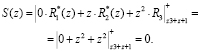
Так как интервал S(z) = 0, то код ПСКВ не содержит ошибки.
Пусть ошибка произошла по первому основанию. Тогда А(z)=(1, z, z2). Определим значение S(z), используя выражение (16). Получаем
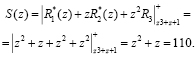
Так как значение полиномиальной формы позиционной характеристики интервала 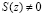 , то код ПСКВ содержит ошибку. Произведем ее исправление. Преобразователь кода ПСКВ в позиционный код определяет значение
, то код ПСКВ содержит ошибку. Произведем ее исправление. Преобразователь кода ПСКВ в позиционный код определяет значение
A*(z)=(α1(z)B1(z)+ α2(z)B2(z) α3(z)B3(z))mod z7+1 =
= ((z6+ z5+ z4+ z3+ z2+z+1)+z(z6+z5+z3+1)+z2(z4+z2+z+1))mod z7+1 =
= (z7+z6+z5+z4+1) mod z7+1= z6+z5+z4.
Тогда для исправления ошибки вычисляем
А(z)=А*(z)+ ΔAj(z) = (z6+z5+z4)+(z6+z5+z4+z3+z2+z+1)= =z3+z2+z+1.
Заключение
В работе показана целесообразность использования модулярных кодов при построении отказоустойчивой системы опознавания «свой-чужой». Представлен алгоритм работы запросно-ответной системы, которая использует коды СОК. Проведенные исследования показали, что применение модулярного кода позволяет не только повысить скорость реализации данной информационной технологии за счет параллельных вычислений по основаниям, но и корректировать ошибки, которые возникают из-за сбоев и отказов в процессе работы. Представлены примеры выполнения протокола аутентификации КА и обнаружения и коррекции ошибок, возникающих в работе системы опознавания «свой-чужой», функционирующей в модулярных кодах.
Библиографическая ссылка
Калмыков М.И., Зеленский М.Д., Денисенко В.В., Калмыков И.А., Алиев Г.С., Ефременков И.Д. РАЗРАБОТКА ОТКАЗОУСТОЙЧИВОЙ ЗАПРОСНО-ОТВЕТНОЙ СИСТЕМЫ АУТЕНТИФИКАЦИИ СПУТНИКА, ФУНКЦИОНИРУЮЩЕЙ В МОДУЛЯРНЫХ КОДАХ // Международный журнал прикладных и фундаментальных исследований. – 2017. – № 7-2. – С. 176-180;URL: https://applied-research.ru/ru/article/view?id=11715 (дата обращения: 24.04.2024).

