Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Фомин А.С. 1

---

1 ФГБОУ ВО «Сибирский государственный индустриальный университет»

Настоящее исследование посвящено структурному анализу манипуляторов с круговой направляющей. В работе проанализированы три типа манипуляторов, в каждом из них выходное звено, выполненное в виде платформы, соединено со стойкой шестью кинематическими цепями. При этом стойка выполнена в виде замкнутой круговой направляющей, на которой установлены шесть кареток, выполняющих роль ведущих звеньев. Выходные звенья в рассматриваемых манипуляторах имеют шесть степеней свободы – они могут вращаться и смещаться относительно каждой из осей декартовых координат, а также совершать полный оборот вокруг оси, перпендикулярной основанию. В каждом из исследуемых манипуляторов выделены ведущие звенья и соединяющиеся с ними кинематические цепи параллельной структуры, определена подвижность манипуляторов. С учетом выполненного структурного анализа могут быть синтезированы новые кинематические схемы манипуляторов параллельной структуры с меньшим числом приводов, а также с заданными траекториями движения выходных звеньев.

Статья в формате PDF

2520 KB

звено

механизм

манипулятор

подвижность

параллельная структура

кинематическая пара

1. Kong X., Gosselin C.M. Type Synthesis of Parallel Mechanismsю Springer Berlin Heidelberg. – 2007. – 272 p.

2. Возможные применения механизмов параллельной структуры / С.В. Хейло [и др.] // Проблемы машиностроения и надежности машин. – 2013. – № 5. – С. 19–24.

3. Развитие исследований механизмов параллельной структуры / В.А. Глазунов [и др.] // Проблемы машиностроения и надежности машин. – 2014. – № 3. – С. 37–43.

4. Глазунов В.А. Структура пространственных механизмов. Группы винтов и структурные группы / В.А. Глазунов // Справочник. Инженерный журнал с приложением. – 2010. – № 3. – С. 15–24.

5. Анализ элементарных перемещений манипулятора параллельной структуры с круговой направляющей на основе дифференцирования уравнений связей / А.К. Алешин [и др.] // Проблемы машиностроения и надежности машин. – 2016. – № 5. – С. 17–21.

6. Кинематический анализ пространственного механизма параллельной структуры с круговой направляющей / Г.В. Рашоян [и др.] // Проблемы машиностроения и автоматизации. – 2014. – № 2. – С. 20–26.

7. Janabi-Sharifi F., Shchokin B. A rotary parallel manipulator: Modelling and workspace analysis. Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), New Orleans, LA. – 2004. – Р. 3671–3677.

8. Shchokin B., Janabi-Sharifi F. Design and kinematic analysis of a rotary positioner. Robotica. – 2007. – Vol. 25. – Р. 75–85.

9. Coulombe J., Bonev I.A. A new rotary hexapod for micropositioning. Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany. – 2013. – Р. 877–880.

10. Fomin A., Glazunov V., Didenko V., Paik J. The design of a new rotary hexapod with a single active degree of freedom. Proceedings of the 5th IFToMM International Symposium on Robotics & Mechatronics (ISRM2017), Sydney, Australia.

11. А.с. 1049244 СССР, МПК B 25 J 1/02. Манипулятор / Беликов В.Т., Власов Н.А., Заблонский К.И., Корытин А.М., Щекин Б.М. – 3392819/25-08; заявлено 11.02.82; опубл. 23.10.83, Бюл. 39. – С. 4.

12. Dvornikov L., Fomin A. Development of the basic conditions for division of mechanisms into subfamilies. Procedia Engineering. – 2016. – Vol. 150. – Р. 882–888.

13. Fomin A., Dvornikov L., Paik J. Calculation of the general number of imposed constraints of kinematic chains. Procedia Engineering. – 2017. – Vol. 206. – Р. 1309–1315.

14. Patent 6196081 US, IPC B25J 17/02, G056 11/00. Systems and methods employing a rotary track for machining and manufacturing / Hexel Corporation, 2001.

15. Разработка одноподвижного механизма параллельной структуры с круговой направляющей / А.С. Фомин [и др.] // Материалы международной научной конференции «Колебания и волны» под ред. Р.Ф. Ганиева. – 2017. – С. 155–157.

Для высокоточного автоматизированного производства требуется, чтобы положение инструмента было точно задано в пространстве. Однако не все механические системы на сегодняшний день могут обеспечить необходимую точность. Это, в частности, связано с ограниченным диапазоном движений выходного звена, высокой стоимостью элементов конструкции и неспособностью воспроизведения заданной траектории движения выходного звена. Для выполнения операций, требующих высокой точности, наиболее подходят механические системы, имеющие параллельную структуру [1–4]. Они также достаточно эффективны и для выполнения операций, требующих быстродействия, максимальной подвижности выходного элемента, повышенной жесткости и других важных показателей для эффективного выполнения технологических операций. Большая часть роботизированных систем параллельной структуры основаны на гексаподах. Гексапод представляет собой механическую систему, имеющую шесть независимых кинематических цепей, которые поворачивают и перемещают выходное звено на различные углы и расстояния относительно стойки. На сегодняшний день основными производителями гексаподов являются Германия (в частности, компания Physik Instrumente), Франция (в частности, компания Symetrie) и США (в частности, компании Newport, Microlar, ALIO Industries), в том числе производящие высокоточные гексаподы. Почти все производимые гексаподы имеют телескопические ножки, что является причиной наличия относительно небольшого рабочего пространства. Как правило, эти гексаподы обеспечивают поворот платформы не более, чем на 30 градусов. В некоторых практических приложениях этого явно недостаточно, поэтому Physik Instrumente (Германия) и ALIO Industries (США) производят также и вращающиеся шестигранники (с выдвижными ногами), которые либо установлены на поворотной ступени, либо в них на подвижной платформе установлена поворотная ступень.

Вместе с тем полный поворот платформы (на 360 градусов) вокруг вертикальной оси является важным свойством и позволяет расширить области применения гексаподов. В частности, они могут применяться в качестве устройств для пространственной ориентации объектов, основы для медицинских роботов, реабилитационных устройств или тренажеров транспортных средств. Например, в работах [5, 6] авторами разработаны и исследованы манипуляторы параллельной структуры с полным вращением выходного звена для применения в автомобильных тренажерах. Полное вращение платформы относительно основания осуществляется с помощью круглого рельса, установленного на стойке. Синтез и анализ манипуляторов параллельной структуры с круговой направляющей также рассмотрены в работах [7–10].

В настоящем исследовании обратимся к анализу структуры манипуляторов с круговой направляющей, в которых подвижная платформа соединена с тремя парами кинематических цепей, включающих разные типы шарниров. Соединенные с платформой кинематические цепи в таких манипуляторах образуют подвижный треугольник, служащий опорой для платформы. Каждая кинематическая цепь, расположенная между основанием и платформой, приводится в движение отдельным двигателем, каждый из которых устанавливается в разнесенных друг от друга местах так, чтобы двигатели могли выполнять перемещения каждой из кинематических цепей. Таким образом, объект, установленный на платформе, может быть перемещен с высокой точностью и с полным диапазоном степеней свободы. Рассмотрим основные известные манипуляторы параллельной структуры с круговой направляющей.

Структурный анализ пространственного манипулятора

Один из первых манипуляторов параллельной структуры с круговой направляющей был разработан в 1983 году Т.В. Беликовым и др. [11] и послужил основой для создания последующих моделей манипуляторов этого класса. На рис. 1, a показана кинематическая схема данного устройства. В нем число подвижных звеньев равно шестнадцати (n = 16), число пар пятого класса равно двенадцати (p5 = 12) и пар третьего класса равно девяти (p3 = 9). В соответствии с формулой А.П. Малышева [12, 13], имеющей вид

(*)

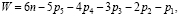где W – подвижность механической системы, определяющая число его степеней свободы, n – число подвижных звеньев механической системы, р5, р4, р3, р2 и р1 – число одно-, двух-, трех-, четырех- и пятиподвижных кинематических пар, подвижность манипулятора будет равна W = 9. Такой результат включает в себя:

1) шесть активных подвижностей, задаваемых шести кареткам, движущимся по круговой направляющей;

2) три пассивных подвижности от трех звеньев, сопряженных с платформой – каждое из них имеет независимое вращение в силу того, что ось сферический шарнир и две сопряженные вращательные пары имеют общую ось вращения.

Рис. 1. Кинематическая схема пространственного манипулятора (a); пространственная кинематическая цепь параллельной структуры (б)

При выделении из цепи манипулятора стойки с ведущими звеньями (каретками) получим пространственную кинематическую цепь, приведенную на рис. 1 , б. Ее подвижность равняется трем (W = 3), т.е. присутствуют три независимых вращения звеньев, соединенных с платформой, вокруг их продольных осей.

Структурный анализ гексапода с двойной круговой направляющей

На рис. 2, a показана кинематическая схема гексапода [9], в котором для увеличения рабочей области добавлена дополнительная круговая направляющая в виде круглого рельса. Такое конструктивное решение позволяет увеличить рабочее пространство данного манипулятора, при этом гарантирована высокая точность. Также в манипуляторе обеспечивается увеличенное смещение платформы в направлении вертикальной оси, когда каретки попарно расположены на соседних рельсах, по сравнению с манипуляторами, где используется одна круговая направляющая.

Обратимся к рассмотрению структуры данного манипулятора. В нем на неподвижном звене (стойке) установлено шесть кинематических цепей, обеспечивающих три выхода на платформу. Каждая пара кинематических цепей включает в свой состав каретки, выполняющие роль ведущих звеньев, на которые устанавливаются соединительные кинематические цепи, удерживающие выходное звено. Все кинематические пары в манипуляторе выполнены вращательными. Гексапод может быть использован в качестве устройства для пространственной ориентации объектов, для восстановительных постоперационных процедур, в автомобильных и летательных тренажерах, для наклона и перемещения обрабатываемых деталей и других практических приложениях.

Обратимся к структурному анализу гексапода. Он включает в свой состав кроме неподвижного звена тридцать одно подвижное звено (n = 31) и тридцать шесть кинематических пар пятого класса (р5 = 36). Подвижность манипулятора при данных параметрах по формуле (*) равна шести (W = 6). Такой результат означает, что для получения требуемого движения выходного звена (платформы) нужно задать движения шести входным звеньям (кареткам), перемещающимся по круговой направляющей.

Выделим в структуре гексапода группу нулевой подвижности. Для этого, с учетом результата, полученного по формуле (*), исключим из кинематической цепи шесть ведущих звеньев и шесть кинематических пар, которыми они соединяются со стойкой. Тогда найдем, что группа нулевой подвижности будет включать двадцать пять звеньев (n = 25) и тридцать кинематических пар пятого класса (р5 = 30). На рис. 2, б показана данная группа. По формуле (*) число степеней свободы этой группы равно нулю (W = 0). Найденная группа нулевой подвижности может быть использована при синтезе новых манипуляторов и роботов параллельной структуры.

Рис. 2. Кинематическая схема гексапода с двойной круговой направляющей (a); пространственная группа нулевой подвижности с вращательными кинематическими парами (б)

Рассмотренный гексапод с двойной круговой направляющей обладает большим рабочим пространством и потенциально более высокой точностью по сравнению с аналогами, имеющими одну круговую направляющую. В связи с этим применение этого манипулятора для операций, требующих высокую точность, достаточно эффективно.

Структурный анализ ротопода

Следующим примером манипулятора параллельной структуры с круговой направляющей является ротопод [13], показанный на рис. 3, a, разработанный американской компанией Hexel, в настоящее время Microlar [14]. В ротоподе кроме вращательных кинематических пар, соединяющих каретки с круговой направляющей, присутствуют и сферические пары. Всего манипулятор включает тринадцать подвижных звеньев (n = 13), соединенных шестью вращательными (р5 = 6) и двенадцатью сферическими (р3 = 12) кинематическими парами. Соответственно, при данных параметрах подвижность ротопода по формуле (*) равна W = 12. Полученный результат означает, что шесть подвижностей имеют ведущие звенья (каретки), а оставшиеся шесть являются пассивными, возникающими из-за поворота каждого из звеньев, оканчивающихся сферическими парами, вокруг их продольных осей.

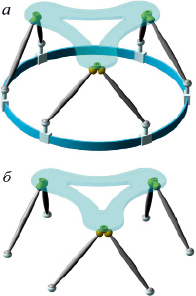
Рис. 3. Кинематическая схема ротопода (a); пространственная кинематическая цепь параллельной структуры (б)

Выделим в ротоподе группу звеньев, соединяющихся с каретками. Она приведена на рис. 3, б, и включает в свой состав семь звеньев (n = 7) и двенадцать сферических кинематических пар (р3 = 12). Подвижность этой группы звеньев по формуле (*) равна шести (W = 6), т.е. каждое из звеньев, соединяющихся с платформой, имеет по одной степени свободы и может поворачиваться вокруг своей продольной оси. Таким образом, приведенная на рис. 3 пространственная кинематическая цепь при соединении с ведущими звеньями образует манипулятор параллельной структуры.

Заключение

В настоящей работе были рассмотрены кинематические схемы известных манипуляторов параллельной структуры с круговой направляющей, обеспечивающие позиционирование и ориентацию рабочей поверхности посредством кинематических цепей, установленных между выходным звеном и стойкой.

Выполнен структурный анализ данных манипуляторов и определена их подвижность. Следует отметить, что для увеличения рабочей зоны выходного звена целесообразно установить на стойке вторую направляющую и, таким образом, расположить каретки попарно на обоих направляющих. Это также позволит увеличить высоту подъема платформы (вертикальное расстояние от стойки до платформы) при неизменных длинах звеньев параллельных кинематических цепей.

Следует отметить также возможность синтеза манипуляторов параллельной структуры с круговой направляющей, имеющих единственный привод и способных направлять выходное звено по разным траекториям. В этом случае с найденными пространственными кинематическими цепями параллельной структуры (рис. 1, б, 2, б, 3, б) должны соединяться одноподвижные механические системы. Такое конструктивное решение обеспечит всей системе единственную степень подвижности [15].

Работа выполнена в рамках Стипендии Президента Российской Федерации (код проекта СП-3755.2016.1).

Библиографическая ссылка