Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Сенницкий В.Л. 1, 2

---

1 Институт гидродинамики им. М.А. Лаврентьева СО РАН

2 Новосибирский государственный университет

Поставлена и решена задача о плоском течении вязкой несжимаемой жидкости между абсолютно твердыми стенками. Силовые воздействия, поддерживающие движение жидкости, отсутствуют; движение жидкости является затухающим. Найдено точное решение задачи. Определены интегральные параметры течения жидкости. Получены асимптотические формулы, характеризующие рассматриваемую гидромеханическую систему на больших временах. Задачи о плоском движении вязкой жидкости в присутствии твердых стенок неизменно входят в число актуальных задач гидромеханики. Результаты исследований плоских течений представляют самостоятельный интерес, а также могут служить в качестве важных ориентиров при изучении пространственных течений. В частности, в связи с этим является актуальным эффективный поиск новых адекватных гидромеханических задач. Одно из перспективных направлений в механике вязкой жидкости, включающее такой поиск, состоит в изучении эволюции гидромеханических систем после прекращения силовых воздействий, поддерживающих их движение. Особая роль в таких исследованиях принадлежит нахождению точных решений задач механики вязкой жидкости. Актуальность работ в данной научной области, в частности, обусловлена их очевидной прикладной значимостью, наличием связи с широким спектром явлений и процессов.

Статья в формате PDF

732 KB

асимптотические формулы

остаточная масса жидкости

твердые стенки

стационарное периодическое затухающее течение

вязкая жидкость

1. Сенницкий В.Л. О силовом взаимодействии шара и вязкой жидкости в присутствии стенки // Прикладная механика и техническая физика. 2000. Т. 41, № 1. С. 57–62.

2. Сенницкий В.Л. Движение вязкой жидкости и стенки в присутствии покоящейся стенки // Прикладная механика и техническая физика. 2016. Т. 57, № 2. С. 76–82. DOI: 10.15372/PMTF20160208.

3. Аристов С.Н., Князев Д.В. Течения вязкой жидкости между подвижными параллельными плоскостями // Известия РАН. Механика жидкости и газа. 2012. № 4. С. 55–61.

4. Петров А.Г. Точное решение уравнений Навье – Стокса в слое жидкости между движущимися параллельно пластинами // Прикладная механика и техническая физика. 2012. Т. 53, № 5. С. 13–18.

5. Петров А.Г. О точных и асимптотических решениях уравнений Навье – Стокса в слое жидкости между сближающимися и удаляющимися плачтинами // Известия РАН. Механика жидкости и газа. 2014. № 2. С. 44–57.

6. Педли Т. Гидродинамика крупных кровеносных сосудов. М.: Мир, 1983. 400 с.

Выявлению закономерностей движения жидкости в присутствии твердых стенок посвящено значительное число исследований (см., например, [1, 2], а также [3–5], и представленную там литературу).

В данной работе рассматривается гидромеханическая система, состоящая из вязкой несжимаемой жидкости и абсолютно твердых стенок Ξ1, Ξ2. Стенки покоятся относительно инерциальной прямоугольной системы координат XYZ. Стенка Ξ1 ограничена плоскостью Γ1: Y = 0; стенка Ξ2 – плоскостью Γ2: Y = H (H > 0 – постоянная). Жидкость заполняет область Ω: 0 < Y < H. В начальный момент времени t, при t = 0, течение жидкости является симметричным относительно плоскости Y = H / 2; жидкость движется со скоростью V0 = {V0(Y), 0, 0} (V0(Y) = V0(H – Y); V0 = 0 на Γ1, Γ2).

Цель данной работы состоит в определении скорости жидкости V = {V(Y, t), 0, 0}, а также силового взаимодействия жидкости и стенок, средней скорости жидкости, массопереноса жидкости – при t > 0.

Общая задача

Пусть y = Y / H; ,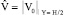
если 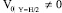, 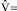sup│V0│, если ; τ = 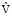t / H; v0 = V0/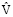; v = V/;
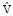ν – кинематический коэффициент вязкости жидкости; Re = H 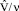 – число Рейнольдса.

Уравнение Навье – Стокса и условия, которые должны выполняться на границах стенок и в начальный момент времени, имеют следующий вид:

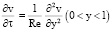; (1)

v = 0 при y = 0; (2)

v = 0 при y = 1; (3)

v = v0 при τ = 0. (4)

Отметим, что при t > 0 какие-либо воздействия на жидкость, поддерживающие ее движение, отсутствуют.

Наряду с задачей (1)–(4) будем рассматривать также вспомогательную задачу

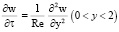; (5)

w = 0 при y = 0; (6)

w = 0 при y = 2; (7)

w = w0 при τ = 0. (8)

Здесь w0 – периодическая с периодом 2 функция y, которая при 0 ≤ y ≤ 2 определяется формулой

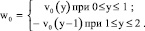(9)

Обратимся к задаче (5)–(7). Применяя метод разделения переменных, найдем, что уравнение (5) имеет последовательность решений

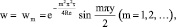(10)

каждое из которых удовлетворяет условиям (6), (7). Используя (10), построим следующее решение задачи (5)–(7):

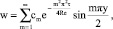(11)

где cm (m = 1, 2, …) – постоянные.

Рассмотрим условие (8). Представим w0(y) в виде ряда Фурье. С учетом (9) и соотношения

v0(y) = v0(1 – y) (12)

получим

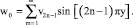(13)

Здесь

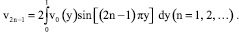
Используя (11), (13) и формулу

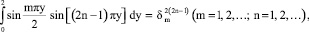
найдем

cm = 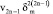(m = 1, 2, … ; n = 1, 2, …). (14)

Из (11), (14) следует, что w (решение задачи (5) – (8)) удовлетворяет условию

w = 0 при y = 1. (15)

Таким образом, согласно (1)–(9), (11), (14), (15) задача (1)–(4) имеет решение

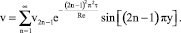(16)

Формулой (16), в частности, демонстрируется, что изучаемое течение жидкости является затухающим.

Пусть ρ – плотность жидкости; γ1 – площадка площадью Sγ, принадлежащая плоскости Γ1; γ2 – площадка площадью Sγ, принадлежащая плоскости Γ2; Flw1 = {Flw1, 0, 0} – тангенциальная сила, действующая со стороны жидкости на часть ξ1 стенки Ξ1, граничащую с жидкостью на площадке γ1 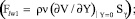Fwl1 = {Fwl1, 0, 0} – тангенциальная сила, действующая со стороны части ξ1 стенки Ξ1 на жидкость; Flw2 = {Flw2, 0, 0} – тангенциальная сила, действующая со стороны жидкости на часть ξ2 стенки Ξ2, граничащую с жидкостью на площадке γ2 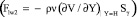; Fwl2 = {Fwl2, 0, 0} – тангенциальная сила, действующая со стороны части ξ2 стенки Ξ2 на жидкость; flwk = HFlwk / (ρ ,
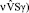fwlk = HFwlk / (ρ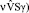 (k = 1, 2); σ – площадка: X = X*, 0 ≤ Y ≤ H , – Z*/2 ≤ Z ≤ Z*/2 (X*, Z* > 0 – постоянные); Sσ = H Z*;

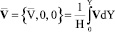(17)

– среднее значение скорости V по координате Y;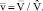

Используя (16), (17), получим

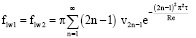(18)

(fwl1 = – flw1, fwl2 = – flw2);

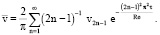(19)

Формулой (18) определяется силовое взаимодействие жидкости и стенок (вопрос о нормальном силовом взаимодействии жидкости и стенок является тривиальным).

Движение жидкости сопровождается переносом ее массы. Мерой происходящего массопереноса может служить остаточная масса жидкости

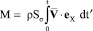(20)

– масса жидкости, которая протекает через площадку σ из области X < X* в область X > X* за промежуток времени 0÷t (eX = {1, 0, 0}) . Используя (17), (19), (20), найдем

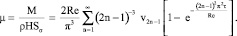(21)

Из (16), (18), (19), (21) следуют асимптотические формулы, характеризующие рассматриваемую гидромеханическую систему на больших временах

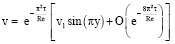при τ → ∞; (22)

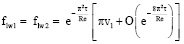при τ → ∞; (23)

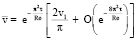при τ → ∞; (24)

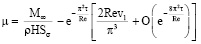при τ → ∞. (25)

Здесь

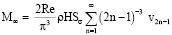(26)

– полная остаточная масса жидкости (предел Μ при t → ∞). Отметим, что ряд в (26) является абсолютно сходящимся (данный ряд мажорируется сходящимся рядом .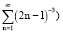

Первая частная задача

Пусть жидкость совершает движение со скоростью U = {U, 0, 0}, не изменяющейся со временем; задача о течении жидкости имеет вид

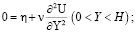(27)

U = 0 при Y = 0; (28)

U = 0 при Y = H. (29)

Здесь η = – (1/ρ) ∂P /∂X – постоянная (P – давление в жидкости; без умаления общности может быть принято, что η > 0). Использование (27)–(29) приводит к формуле

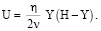(30)

Положим

V0 = U. (31)

Отметим, что

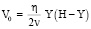
удовлетворяет соотношению (12).

Выполнение (31) соответствует тому, что задачей (1)–(4), определяемым ею течением жидкости моделируется происходящее при t > 0 остаточное, не поддерживаемое силовыми воздействиями затухающее течение вязкой жидкости, совершающей при t ≤ 0 движение с не изменяющейся со временем скоростью

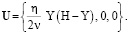
С учетом (16), (17), (19)–(21), (26), (30), (31) для данного (моделирующего) течения жидкости, в частности, имеем

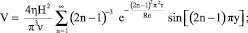
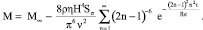
Здесь

,

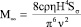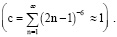
Вторая частная задача

Пусть жидкость совершает движение со скоростью U2 = {U2, 0, 0}, периодически изменяющейся со временем; задача о течении жидкости имеет вид

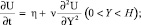(32)

U = 0 при Y = 0; (33)

U = 0 при Y = H. (34)

Здесь η = ξ [1 + sin(2πt / T + φ)] (ξ, T > 0. 0 ≤ φ < 2π – постоянные; без умаления общности может быть принято, что ξ > 0). Использование (32)–(34) приводит к формуле

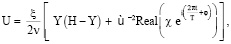(35)

где χ = {sh[(1 + i)ϰY] + sh[(1 + i)ϰ(H – Y)] – sh[(1 + i)ϰH]} / sh[(1 + i)ϰH];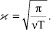

Положим

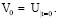(36)

Отметим, что

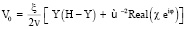
удовлетворяет соотношению (12) .

Выполнение (36) соответствует тому, что задачей (1) – (4), определяемым ею течением жидкости моделируется происходящее при t > 0 остаточное, не поддерживаемое силовыми воздействиями затухающее течение вязкой жидкости, совершающей при t ≤ 0 движение с периодически изменяющейся со временем скоростью

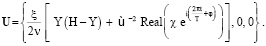
С учетом (16), (17), (19)–(21), (26), (35), (36) для данного (моделирующего) течения жидкости, в частности, имеем

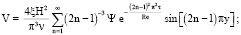
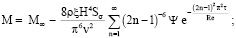
Здесь

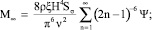
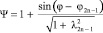(λ2n – 1 = 2H2 / [(2n – 1)2πνT]; 0 < φ2n – 1 < π /2 (n = 1, 2, …) – углы, удовлетворяющие соотношениям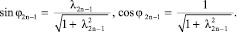

Заключение

Исследованное течение жидкости является аналогом пространственного течения вязкой жидкости в бесконечно длинной круговой цилиндрической трубе. В моменты времени, следующие за начальным, жидкость не испытывает каких-либо силовых воздействий, поддерживающих ее движение. Ввиду этого представляют очевидный интерес, могут быть отмечены постановка вопроса об остаточной массе жидкости, установление зависимости этой величины от времени и параметров гидромеханической системы, определение полной остаточной массы жидкости – важной характеристики рассмотренной гидромеханической системы. Полученные результаты могут найти применение при разработке новых приборов, устройств, содержащих жидкости, могут использоваться при изучении проблем биологии, медицины, связанных с движением жидких сред, в частности проблем патологии и нормы крово-
обращения [6].

Библиографическая ссылка