Чебышевскими называют сети с равносторонними четырехугольными ячейками [1]. Они хорошо моделируют формообразующие свойства тонких ортотропных материалов, таких как ткани, так как способны гладко укладываться на поверхностях двоякой кривизны за счет изменения угла между нитями [2]. Поэтому их используют для расчета раскроя тканевых оболочек.
Положение сети, наложенной на криволинейную поверхность можно описать совокупностью координат ее узлов. Представим, что в эвклидовом пространстве, центр сферы совмещен с началом координат. Сеть Чебышева принято ориентировать на поверхности так, чтобы исходные направления нитей располагались по взаимно ортогональным геодезическим линиям. Начинать накладывать сеть удобно с точки зенита, координаты которой X=0, Y=0, Z=R. Здесь R – радиус сферы. Совмещаем нити сети с направлениями меридиан в плоскостях X0Z и Y0Z, являющихся геодезическими линиями на сфере. Координаты узлов сети, размещенных на этих меридианах, можно вычислить по формулам (1):
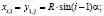
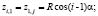(1)
где i и j – порядковые номера узлов сети по направлениям меридиан вдоль осей X и Y, соответственно, при этом в точке зенита их значения равны 1;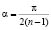 
– величина дуги между узлами сети в радианах; n – количество узлов сети Чебышева на осевом меридиане.
Задачу вычисления координат узлов сети на сфере, расположенных между осевыми меридианами, можно сформулировать как последовательное отыскание координат четвертых узлов пространственно криволинейных равносторонних четырехугольников ячеек сети, по известным координатам двух смежных узлов. Заметим, что на сфере равенство длин дуг означает и равенство их хорд. Заменим рассмотрение пространственно – криволинейной ячейки сети исследованием ее модели в виде ломанного пространственного параллелограмма. Для искомого узла, как точки пересечения в пространстве двух отрезков смежных сторон параллелограмма можно записать требование совместности двух нелинейных уравнений 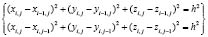(2).
, (2)
где h – хорда, как кратчайшее расстояние между смежными узлами ячейки сети. Это расстояние легко вычисляется по формуле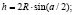 
Решением системы (2) должно являться уравнение окружности, как линии пересечения двух сфер радиуса h с центрами в узлах, смежных с искомым.
Условие того, что искомый узел лежит на поверхности сферы, запишем в виде уравнения сферы радиуса R 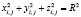(3)
. (3)
Это уравнение имеет два корня и определяет, что искомый узел может находиться в одной из двух точек пересечения указанной выше окружности с поверхностью сферы. Очевидно, что эти точки, суть две противоположные вершины ячейки, положение одной из которых заведомо определено.
Произведем упрощения системы (2), раскрыв скобки и учитывая, что сумма квадратов координат каждого из узлов равна квадрату радиуса сферической поверхности с центром в начале координат (4). Это приводит систему к двум линейным уравнениям 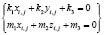(4):
, (4)
где, для упрощения введены коэффициенты, вычисляемые по формулам 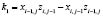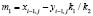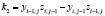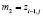(5):
; 
;
; 
; (5)
;
.
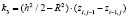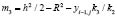Переписав уравнения (4), в виде функций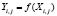 
; 
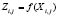и, подставив их в уравнение (3), получим квадратное уравнение с одним неизвестным 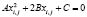(6)
. (6)
Здесь коэффициенты A, B и свободный член C введены для упрощения записи и вычисляются по формулам (7), с учетом (5).
; 
; 
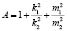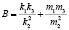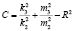. (7)
Таким образом, для вычисления координат узлов сети Чебышева на сфере достаточно найти больший из корней Хi,j уравнения (6) и подставляя его значение в уравнения (4) вычислить значения координат Yi,j и Zi,j. Заметим, что в связи с симметрией достаточно вычислить координаты половины узлов, так как:
; 
; 
.
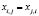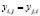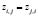Полученные автором формулы, в качества эксперимента, были использованы для вычисления плоской развертки сферы. Форма вычисленной развертки оказалась аналогичной развертке, построенной по методу Чебышева и описанной в целом ряде публикаций о кройке одежды [3].
Библиографическая ссылка
Удлер Е.М. СЕТЬ ЧЕБЫШЕВА НА ПОВЕРХНОСТИ СФЕРЫ // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 6. – С. 43-44;URL: https://applied-research.ru/ru/article/view?id=5164 (дата обращения: 24.04.2024).