Для целей формализации конечных объектов и процессов, оперирующих символьной информацией, разработан универсальный аппарат на базе алгебры конечных предикатов [1]. Этот аппарат развивается около 50 лет и за это время доказал свою эффективность в области теории искусственного интеллекта [2].
Алгебра конечных предикатов является полной, т.е. ее средствами можно описывать любые конечные отношения. Однако информационные процессы – это не только конечные отношения, но и действия над ними. Аппаратом второй ступени является алгебра предикатных операций. Язык алгебры предикатных операций тоже универсален, но он используется для выражения действий над отношениями.
Теория конечных предикатов имеет некоторые результаты по декомпозиции предикатов, т.е. взаимно однозначного преобразования предикатов одной размерности в предикаты другой размерности. Преобразование системы предикатов, имеющих, вообще говоря, произвольную конечную размерность, в систему бинарных предикатов дает ряд преимуществ при моделировании информационных объектов и процессов. Основное из них – возможность перехода от последовательного алгоритмического вычисления к параллельному, что важно при решении задач, требующих больших объемов вычислений. Графическое представление системы бинарных предикатов называется логической сетью.
Логическая сеть состоит из полюсов и ветвей, ветви соединяют полюсы. Каждому полюсу соответствует своя предметная переменная хi с областью определения 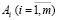 . Пара полюсов хi и хj, соединенных ветвью K (хi, хj), реализуют линейный логический оператор первого рода.
. Пара полюсов хi и хj, соединенных ветвью K (хi, хj), реализуют линейный логический оператор первого рода.
Рассматриваемый аппарат предназначен для решения задач идентификации структур в области искусственного интеллекта [1, 2]. Однако традиционные логические сети не предназначены для обработки структур, отражающих выполнение процессов произвольной физической природы (процессы мышления, производства, поиска данных в сети интернет и т.п.), поскольку последние обязательно направлены во времени. Такие процессы могут быть представлены в виде последовательности событий, каждое из которых обладает временной меткой. Следует отметить, что важно не абсолютное значение, задаваемой временной меткой, а порядок событий (действий процесса).
В связи с изложенным возникает проблема предикатного описания процессов произвольной физической природы на основе логических сетей, рассмотрению которой и посвящена данная работа.
1. Анализ работ в данной области
В работе [3] был рассмотрен способ построения и настройки модели гибкого процесса и детализированы особенности этапа адаптации модели. Модель гибкого процесса, адаптированной к предметной области, в общем виде представлена системой бинарных предикатов
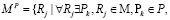
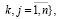 (1)
(1)
где Rj – бинарные предикаты, а Pk – объекты предметной области.
В статье [4] предложена предикатная процессная модель на основе дерева процессов и аппарата конечных предикатов. Предложенный метод позволяет объединить базовые способы слияния логов и построения модели процесса средствами process mining. Были введены два типа узлов логической сети. Вершины первого типа x∈V* отражают конкретные действия (процедуры) процесса. С каждой вершиной связаны определенные действия процесса с помощью бинарных предикатов:
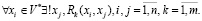
Соответственно, модель (1) дополняется следующим образом:
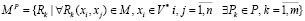 (2)
(2)
Вершина называется вершиной второго типа x′∈V**, если из вершины x′ графа логической сети выходит две дуги. Адаптация процессной модели к предметной области достигается за счет применения известных операторов адаптации базовых элементов модели: последовательное выполнение, выбор, параллельное выполнение, цикл.
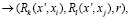 (3)
(3)
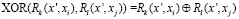
или
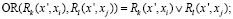 (4)
(4)
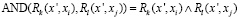 ; (5)
; (5)
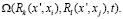 (6)
(6)
В приведенных работах рассмотрено общее представление графа процесса, однако вопросы моделирования таких процессов логической сетью требуют дальнейшего развития.
2. Постановка задачи
Задача данной работы заключается в построении модели логической сети с предикатными операциями вида (3)-(6), для формализации поведения, а также оценки процессов различной физической природы, которые характеризуются заданной последовательностью действий.
2.1 Модифицированная логическая сеть
Вводя в конструкцию логической сети операции типа (3)-(6), мы уходим от общепринятого определения логической сети, как системы бинарных предикатов. Во-первых, логическая сеть – это неориентированный граф, а полученная нами конструкция – ориентированный граф. Во-вторых, мы используем не только бинарные предикаты, но и тернарные. В-третьих, и это, по нашему мнению, основное отличие, в полученной конструкции используются предикатные операции, т.е. предикаты второго порядка [3]. Назовем такую сеть логической сетью с предикатными операциями.
Графически, за счет применения предикатных операций, логическая сеть из плоской становится объемной, рис. 1. Такая конструкция имеет физический смысл, т.к. отражает реальное разделение процедур процесса на элементарные базовые действия и операции над этими процедурами. Полученная модификация логической сети является естественной адаптацией ее структуры для рассматриваемой предметной области – построения гибкой процессной модели.
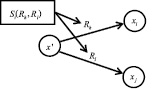
Рис. 1. Логическая сеть с предикатной операцией Si (Rk, Rl)
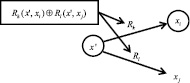
Рис. 2. Эксклюзивный выбор
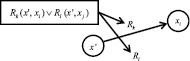
Рис. 3. Неэксклюзивный выбор
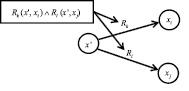
Рис. 4. Параллельное выполнение
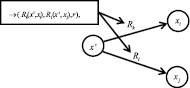
Рис. 5. Последовательное выполнение
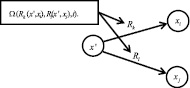
Рис. 6. Предикатное представление цикла
Иллюстрация предикатного представления эксклюзивного и неэксклюзивного выбора, а также параллельного выполнения приведена на рис. 2–6.
Для операторов последовательного выполнения и цикла важно задать порядок вершин (слева-направо) вне зависимости от их типа, поскольку порядок вершин задает порядок выполнения действий процесса:
В случае цикла, одна вершина соответствует началу цикла, содержащему условие повторения (обычно соответствует фрагменту с «do», «for»).
Правая вершина соответствует собственно операции (группе операций) цикла, после которых происходит переход к новому повторению.
В целом модель процесса представляется в виде иерархии предикатных операций вида (3)-(6) на верхних уровнях, а также бинарных предикатов на нижнем уровне:
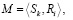
где
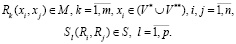 (7)
(7)
Исходя из общих представлений о процессе, полная модель процесса обязательно должна иметь одно начальное и одно конечное состояние, а также содержать пути достижения конечного состояния. Математически это можно описать структурой, имеющей:
– начальную переменную х1 (вход модели);
– конечную переменную хm (выход модели);
– систему бинарных предикатов Rk (хi, хj), описывающих процедуры процесса;
– систему предикатных операций Sl (Ri, Rj);
– матрицу ZR (Rk, t), определяющую последовательность вычисления бинарных предикатов Rk (хi, хj), t – номер такта работы логической сети, число тактов определяется максимальной длиной цепочек процедур в логической сети, моделирующей процесс;
– матрицу ZS (Sl, t), определяющую, как должны применяться предикатные операции Sl (Ri, Rj).
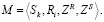 (8)
(8)
3. Пример адаптации модели модифицированной логической сети к предметной области
Рассмотрим пример структуры логической сети с предикатными операциями.
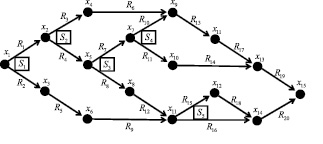
Рис. 7. Логическая сеть с предикатными операциями
Имеем логическую сеть с 15-ю событиями 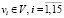 , обозначенными переменными x1, x2,…, x15, 20-ю действиями
, обозначенными переменными x1, x2,…, x15, 20-ю действиями 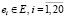 , которые описывают попарные связи между событиями, обозначенными предикатами
, которые описывают попарные связи между событиями, обозначенными предикатами 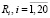 и 5-ю предикатными операциями
и 5-ю предикатными операциями 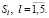
Матрица ZR (Rk, t) для логической сети, изображенной на рис. 7, имеет следующий вид:
Таблица 3
Матрица последовательности вычисления бинарных предикатов Rk
|
k t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
2 |
0 |
0 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
0 |
1 0 |
2 |
2 |
1 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
2 |
1 0 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|||
|
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
Как видно из табл. 3, некоторые действия могут выполняться в течение двух тактов (k = 6, 9, 14, 16). Если несколько действий выполняются на одном и том же такте, можно определить последовательность их выполнения, если это необходимо. Например, на 2-м такте вначале нужно выполнить 4-е действие, затем 3-е. Если последовательность выполнения действий в пределах одного такта не важна, то в матрице ставятся единицы, например, на 1-м такте действия 1 и 2 могут выполняться в любом порядке.
Матрица ZS (Sl, t) для логической сети, изображенной на рис. 7, имеет следующий вид:
Таблица 4
Матрица выполнения предикатных операций Sl (Ri, Rj).
|
l t |
1 |
2 |
3 |
4 |
5 |
|
1 |
1 |
0 |
0 |
0 |
0 |
|
2 |
0 |
1 |
0 |
0 |
0 |
|
3 |
0 |
0 |
1 |
0 |
0 |
|
4 |
0 |
0 |
0 |
1 |
0 |
|
5 |
0 |
0 |
0 |
0 |
1 |
|
6 |
0 |
0 |
0 |
0 |
0 |
|
7 |
0 |
0 |
0 |
0 |
0 |
Матрица выполнения предикатных операций имеет приоритет над матрицей последовательности вычисления бинарных предикатов (в случае конфликта правил). В случае если предикатная операция цикла содержит несколько повторений, то они могут выполняться в течение одного такта логической сети.
При предлагаемом иерархическом предикатном представлении каждый предикат нижележащего уровня соответствует переменной предиката вышележащего уровня и, за исключением нижнего уровня, реализует соответствующую функциональность.
Иерархическое представление гибкого процесса позволяет адаптировать модель к предметной области простым отсечением «избыточных» ветвей путем удаления либо преобразования связанных с вершинами предикатов. В результате последовательность действий процесса корректно упрощается. Адаптация модели к предметной области должна проводиться на основании дополнительных знаний о моделируемом процессе. Рассмотрим процесс адаптации модели на примере логической сети, изображенной на рис. 7. В качестве дополнительных знаний введем стоимость (вес) действий. Кроме того, необходимо учитывать особенности выполнения предикатных операций.
Зададим веса дуг графа логической сети.
Таблица 5
Матрица весов дуг графа логической сети
|
Дуга |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Вес |
1 |
1 |
1 |
2 |
1 |
3 |
1 |
2 |
2 |
1 |
2 |
1 |
3 |
1 |
1 |
2 |
2 |
4 |
2 |
3 |
Найдем наименьший путь на этом графе от x1 к x15. Рассмотрим все варианты таких путей. Через запятую указаны номера дуг графа:
1, 3, 6, 13, 17, 19. Вес равен 12.
1, 4, 7, 10, 13, 17, 19. Вес равен 12.
1, 4, 7, 11, 14, 19. Вес равен 9.
1, 4, 8, 12, 15, 18, 20. Вес равен 14.
1, 4, 8, 12, 16, 20. Вес равен 11.
2, 5, 9, 15, 18, 20. Вес равен 12.
2, 5, 9, 16, 20. Вес равен 9.
Получили два равноценных варианта с весом пути, равным 9 – №3 и №7, рис. 8.
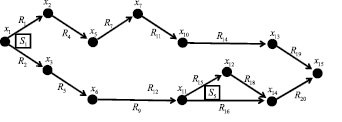
Рис. 8. Минимальные пути на графе логической сети без учета предикатных операций
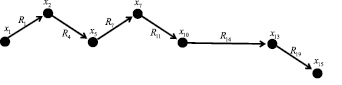
Рис. 9. Минимальный путь на графе логической сети с учетом предикатных операций
Теперь учтем влияние предикатных операций Si. Зададим эти операции. Пусть
S1 = 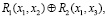
S2 = 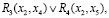
S3 = 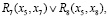
S4 = 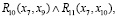
S5 = 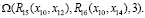
Предикатная операция S1 определяет эксклюзивный выбор между R1 и R2, на вес путей №3 и №7 это не влияет. А предикатная операция S5 задает цикл из трех повторений, что делает вес пути № 7 большим. Поэтому минимальный вес имеет путь № 3:
В результате адаптации модели получили из системы из 20 бинарных предикатов, плюс пяти тернарных предикатных операций систему из 6 бинарных предикатов.
Заключение
В статье предложена модель направленной логической сети с предикатными операциями (предикаты второго порядка) следующих типов: AND, OR, XOR, цикл, последовательность. В отличие от известной модели логической сети, представляющей собой систему бинарных предикатов, предложенная модификация имеет двуслойную структуру – к традиционной модели логической сети добавлен уровень предикатных операций. Разработанная модель обеспечивает возможность формализации поведения, а также оценки процессов различной физической природы, которые характеризуются заданной последовательностью действий или событий, фиксирующих выполнение действий.
Область практического применения предлагаемой модели – интеллектуальный анализ процессов.
Библиографическая ссылка
Рудометкина М.Н., Спицын В.Г. МОДЕЛЬ ЛОГИЧЕСКОЙ СЕТИ С ПРЕДИКАТНЫМИ ОПЕРАЦИЯМИ // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 10-3. – С. 21-26;URL: https://applied-research.ru/ru/article/view?id=6019 (дата обращения: 26.04.2024).

