В последнее время международное образование становится все более актуальным. Многие российские вузы принимают иностранных граждан не только для получения базового образования, но и для подготовки кандидатских диссертаций или профессиональной переподготовки по определенной специализации. Студентам, получающим образование на неродном языке, гораздо сложнее в процессе обучения. Поэтому одной из приоритетных задач высшего образования в России является выявить проблемы, мешающие получать качественное образование иностранным студентам, и найти способы для их решения.
Традиционно наиболее сложными дисциплинами для студентов начальных курсов являются математические дисциплины. Несмотря на то, что язык математики понятен людям, говорящим на любых языках, успеваемость по этим дисциплинам оказывается гораздо ниже, чем по другим дисциплинам. Это обусловлено многими факторами, например, сложностью изучаемого материала, слабой довузовской подготовкой обучающихся, их недостаточной мотивированностью и так далее. Эти вопросы подробно рассматривались в [1].
В процессе перехода российских вузов к уровневой системе – бакалавриат, магистратура – возникла необходимость преобразований как образовательных технологий, так и контрольно-оценочных принципов образовательной деятельности студента. Проблемам оценивания в высшем образовании уделяется достаточно пристальное внимание, так как это непосредственный показатель связи между деятельностью студента и его профессиональным ростом. Главная задача вуза – это организовать условия, в которых наиболее эффективной для студента будет его ритмичная учебная деятельность. В то время как европейские и американские университеты используют различные системы оценивания уже больше 60 лет и до сих пор ведут дискуссии по их совершенствованию [2, 3, 4], для российской высшей школы эта проблема впервые возникла в связи с присоединением к болонскому процессу. На сегодняшний день в российских вузах широко распространилась одна из таких технологий – кредитно-рейтинговая система оценивания. Ее теоретические аспекты подробно описаны в [5]. Здесь объектом контроля и оценки выступает качество освоения курса студентом.
Традиционная система оценивания предполагает единовременный контроль знаний – итоговый экзамен. В таком подходе принцип систематичности контроля не выдерживается. Кроме того, экзамен зачастую имеет обучающую функцию, но не контролирующую. Рейтинговая система контроля имеет ряд преимуществ:
• позволяет поддерживать ритмичную систематическую работу студентов;
• устанавливает обратную связь работы студента и результата этой работы;
• повышает ответственность студента за свое обучение;
• позволяет студенту планировать и предсказывать итоговую оценку;
• стимулирует познавательную и творческую активность и др.
Кроме явных отличительных черт, рейтинговая система является более гибкой для управления образовательным процессом. В зависимости от разработанной системы «как оценивать» и «за что оценивать» можно стимулировать те или иные формы работы, развивать планируемые компетенции.
В 2011 году в Томском политехническом университете было принято решение перейти на кредитно-рейтинговую систему оценивания. Основными этапами контроля и диагностики этой системы можно выделить текущий контроль (баллы за контрольные точки – законченные темы курса и оценка самостоятельной работы студента), рубежный контроль (суммарный рейтинговый балл семестра) и итоговый контроль (аналог традиционного экзамена). Оценка за дисциплину (100 %) вычисляется суммированием баллов за рубежный контроль (60 %) и итоговый контроль (40 %).
В данной работе выявляется зависимость качества математического образования иностранных студентов от выбранной системы оценивания. Обсуждаются две системы оценивания работы студентов: традиционная и рейтинговая. Методами корреляционного анализа проводится сравнительный анализ этих систем и выявляется их эффективность при преподавании высшей математики для иностранных студентов первого года обучения. Исследуются итоговые оценки по математическим дисциплинам различных групп иностранных студентов, обучавшихся в Томском политехническом университете в течение последних пяти лет.
На рисунке представлены результаты средних баллов итоговой оценки за первый и второй семестры за исследуемые пять лет.
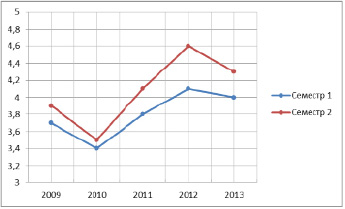
Средняя итоговая оценка за первый и второй семестры
Как видно из рисунка, средняя успеваемость в первом семестре стабильно ниже, чем во втором. Несмотря на то, что в первом семестре изучаются темы уже некоторым образом знакомые студентам из школьного курса (решение систем уравнений, нахождение производных, исследование функций и т.д.) и студенты уже имеют представление об инструментах алгебры и анализа, им необходимо рассматривать материал с обобщенных позиций в рамках единой аксиоматики. Это часто вызывает серьёзные затруднения, поскольку такой род деятельности не практикуется в школьной программе. Кроме того, существенной проблемой является отсутствие умения за короткое время воспринимать и усваивать большие объемы информации. Но как мы видим, качественный результат – умение учиться – начинает проявляться уже во втором семестре. Отметим также, что во втором семестре изучаемые темы базируются на темах первого семестра (интегралы, ряды, дифференциальные уравнения и т.д.). Таким образом, успешность во втором семестре сильно зависит от успешности в первом.
Данные, представленные на рис. 1, показывают, что начиная с 2011 года, когда была введена кредитно-рейтинговая система, наблюдается прогресс в результатах освоения математических дисциплин, как в первом, так и во втором семестре. Особенно это проявляется на итоговой оценке за второй семестр. Такое улучшение частично связано с увеличением составляющей за работу в семестре, то есть суммарный рейтинговый балл за второй семестр преимущественно возрастает. Студенты начинают больше сосредотачиваться на текущих контрольных точках, стараются не терять на них баллы.
Вычисление дисперсии итоговых оценок за каждый семестр показало, что с введением рейтинговой системы этот показатель уменьшился. То есть повышение средней оценки связано не с тем, что отдельные студенты начали показывать выдающиеся результаты, а с тем, что успеваемость улучшилась в целом у всех студентов.
В таблице приведены корреляционные отношения рейтинга за семестр и оценки за экзамен, оценки за экзамен и итоговой оценки.
Коэффициенты линейной корреляции
|
Баллы за семестр и оценка за экзамен |
Оценка за экзамен и результирующая оценка |
|||
|
Семестр 1 |
Семестр 2 |
Семестр 1 |
Семестр 2 |
|
|
2009 |
0.35 |
0.45 |
||
|
2010 |
0.39 |
0.51 |
||
|
2011 |
0.45 |
0.69 |
0.79 |
0.92 |
|
2012 |
0.61 |
0.65 |
0.84 |
0.85 |
|
2013 |
0.53 |
0.61 |
0.82 |
0.91 |
В первые два исследуемых года – 2009 и 2010 – корреляция между средней оценкой за семестр и экзаменационной оценкой достаточно слабая, работа в семестре незначительно влияла на оценку на экзамене. Это преимущественно обуславливается тем, что часть студентов не считали нужным готовиться к текущим контрольным точкам и изучали дисциплину непосредственно перед экзаменом, уже в период сессии. Таким образом, те студенты, которым по каким-либо причинам трудно давалось изучение математики, даже при регулярных и интенсивных занятиях во время семестра, имели мало шансов получить высокую итоговую оценку, поскольку баллы за экзамен у них оказывались также достаточно низкие. Противоположная ситуация складывалась для сильных студентов, которые могли показать хорошие результаты на экзамене, несмотря на то, что в течение семестра мало уделяли времени учебной работе. Однако такое отношение к учебе часто приводило к тому, что эти студенты сильно ухудшали свои оценки во втором семестре.
При рейтинговой системе оценивания, то есть с 2011 года, корреляция между семестровыми баллами и экзаменационной оценкой увеличивается. Такая же тенденция прослеживается и при переходе ко второму семестру.
При переходе к новой системе оценивания у преподавателей возникали опасения, что набрав баллы в течение семестра, студенты не будут уделять должное внимание подготовке к экзамену, что итоговая оценка будет значительно выше оценки за экзамен. Однако из третьего и четвертого столбцов таблицы видно, что коэффициент корреляции между оценкой за экзамен и итоговой оценкой достаточно высок, от 0.79 до 0.92, то есть наблюдается сильная корреляция между этими оценками.
Таким образом, первый этап введения новой системы оценивания приводит к положительным результатам:
• улучшаются результаты обучения;
• наблюдается систематизация учебной работы студентов;
• образовательная нагрузка становится равномерной;
• усиливаются мотивы к постоянной семестровой работе;
• сглаживается разрыв между итоговыми оценками слабых, но упорных студентов и сильных, но не трудоспособных;
• появляется больше возможностей для коррекции имеющихся недочетов.
Возможно, что дальнейшее совершенствование рейтинговой системы поможет детализировать управление образовательной деятельностью студентов, усилить их теоретическую подготовку, активизировать творческую составляющую и приведёт к более качественным результатам обучения.
Библиографическая ссылка
Шерстнёва А.И., Имас О.Н. ПОВЫШЕНИЕ КАЧЕСТВА МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ ИНОСТРАННЫХ СТУДЕНТОВ ПОСРЕДСТВОМ ВЫБОРА СИСТЕМЫ ОЦЕНИВАНИЯ // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 5-4. – С. 573-576;URL: https://applied-research.ru/ru/article/view?id=7169 (дата обращения: 19.04.2024).

