При инженерных расчетах подшипников скольжения для оценки их работоспособности и долговечности в качестве основных критериев используются среднее давление в контакте и произведение этого давления на скорость относительного перемещения контактирующих поверхностей:
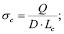 (1)
(1)
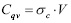 (2)
(2)
где Q – радиальное усилие, действующее на цапфу; D – диаметр отверстия втулки; Lс – длина цапфы, находящаяся в контакте с втулкой; σс – среднее напряжение в контакте; V – скорость перемещения поверхности цапфы относительно поверхности отверстия втулки.
Среднее давление, определяемое по формуле (1) не соответствует действительным значениям в силу двух причин: 1) фактическая площадь контакта цапфы с отверстием втулки не является прямоугольником со сторонами равными диаметру подшипника и длине цапфы (рис. 1 а), а представляет собой часть цилиндрической поверхности (рис. 1 б); 2) контакт цапфы с отверстием втулки осуществляется только на части полной поверхности цапфы с углом охвата 2φк в связи с тем, что она устанавливается в подшипнике с гарантированным зазором, предотвращающим заклинивание и обеспечивающим масляный клин в соединении.
Например характер посадки в в подшипниках скольжения зависит от многих причин. Валы устанавливают в отверстиях подшипников по посадкам: H8/f7; H7/e7; H7/e8; H7/d8; H7/c8. В диапазоне d=20…250 мм значения среднего и относительного зазоров аппроксимируются формулами
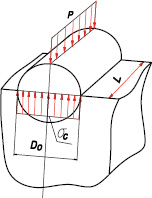
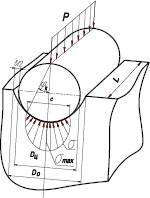
Рис. 1. Установка цапфы во втулке: а – принимаемая для расчета среднего давления σс; б – фактическая схема нагружения
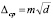 ;
; 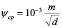 (3)
(3)
где d – диаметр вала; m – постоянная величина, зависящая от посадки:
Посадки c8 d9 d8 f9 e8 f8 f7 f6
m 23 21,5 17 13 12 9 7,5 6
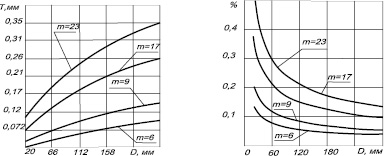
Для каждого конкретного случая существует свое значение оптимального радиального зазора, определяемого расчетом. Основной вопрос сводится к установлению факта насколько формула (1) соответствует реально существующему значению напряжений. Как видно из рис. 2 величина зазора колеблется в довольно широких пределах. Для дальнейших исследований примем минимально возможный диаметральный зазор δ= 0,0025 мм.
а б
Рис. 2. Величина зазора в подшипнике скольжения а – и его процентное отношение; б – в зависимости от диаметра
Значения величин Q и V определяются служебным назначением подшипника и не могут быть изменены.
Из формул (1) и (2) следует, что снижение удельного давления и произведения давления на скорость при заданной радиальной силе возможно только за счет увеличения площади контакта, что влечет за собой увеличение диаметра цапфы и ее длины. Это приводит к изменению габаритов подшипника, во многих случаях недопустимом по различным накладываемым конструктивным и эксплуатационным ограничениям и соображениям. Поэтому необходимы другие пути реализации снижения удельного давления. Целью дальнейших исследований является определение особенностей деформирования цапфы с опорной поверхностью втулки и установление фактических количественных соотношений контакта в зависимости от нагрузки на цапфу и величины зазора в соединении подшипника.
В теории упругости при решении контактных задач для вычисления фактической площади контакта существуют хорошо зарекомендовавшие себя на практике зависимости полученные Герцем [1]
Приняв к сведению, что между диаметрами цапфы и опорной поверхностью отверстия существует зависимость 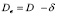 , где Dв и D – диаметр цапфы и диаметр опорной поверхности; δ – диаметральный зазор между цапфой и отверстием втулки, получим на основе элементарных преобразований следующие формулы для определения полуширины контакта и максимальных напряжений в контакте в зависимости от величины диаметрального зазора и диаметров подшипников:
, где Dв и D – диаметр цапфы и диаметр опорной поверхности; δ – диаметральный зазор между цапфой и отверстием втулки, получим на основе элементарных преобразований следующие формулы для определения полуширины контакта и максимальных напряжений в контакте в зависимости от величины диаметрального зазора и диаметров подшипников:
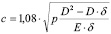 (4)
(4)
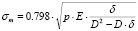 (5)
(5)
Среднее давление, приходящееся на контакт
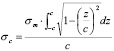 (6)
(6)
Усилие деформирования
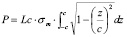 (7)
(7)
Количество тепла выделяемого при трении в контакте
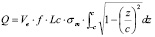 (8)
(8)
или
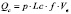
Анализ зависимостей полученных расчетным путем с применением программного обеспечения MathCAD показывает следующее.
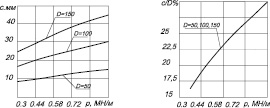
Рис. 3. Изменение ширины контакта между цапфой и отверстием втулки и процентного отношения ширины контакта к диаметру вала в зависимости от удельного усилия деформирования и различных диаметров соединений
Оказалось, что действительная ширина контакта между цапфой и опорным кольцом подшипника существенно меньше диаметра отверстия кольца, который принимают за ширину контакта при расчетах по приведенным в справочникам методиках и не превышает 35% (рис. 3,б). Ширина контакта увеличивается пропорционально увеличению диаметра цапфы (рис.3,а). В то же самое время максимальные напряжения в контакте уменьшаются (рис. 4). Сближение контактирующих поверхностей намного меньше по отношению к радиальному зазору и не превышает шести процентов (рис.4), что позволяет в первом приближении не учитывать его влияние на смещение цапфы.
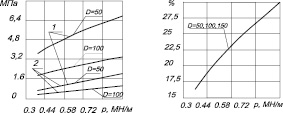
Рис. 4. Изменение максимальных напряжений от погонного давления действующего на вал и диаметров втулки подшипника1- D=50 мм; 2-D= 100мм; 3-D=150 мм
Библиографическая ссылка
Вирт А.Э., Отений Я.Н. ОСОБЕННОСТИ РАСЧЕТА КОНТАКТНЫХ НАПРЯЖЕНИЙ В ЦИЛИНДРИЧЕСКИХ ПАРАХ ТРЕНИЯ // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 9-4. – С. 573-576;URL: https://applied-research.ru/ru/article/view?id=7549 (дата обращения: 25.04.2024).

