Введение
В настоящее время наблюдается бурное развитие информационных технологий и их внедрение в самые различные сферы деятельности человека. С информацией человек имеет дело ежедневно – создает, хранит и обрабатывает, передает ее, используя персональные компьютеры и мобильные устройства. На предприятиях используются специализированные системы хранения и обработки данных, на базе которых функционируют информационные системы, обеспечивающие те или иные бизнес-процессы предприятия.
Особое место в современном мире занимают распределенные системы обработки и хранения данных, в частности, кластеры высокой готовности для систем управления базами данных, обеспечивающие отказоустойчивое хранение и обработку данных. Для таких систем важно знать их показатели надежности для оценки рисков для бизнес-процессов и степени снижения этих рисков за счет применения отказоустойчивых технологий. В такой ситуации разработка моделей надежности и анализ показателей надежности систем обработки данных является достаточно актуальной задачей.
На сегодняшний день существует множество обобщенных моделей надежности и методов расчетов показателей надежности, изложенных в отечественной литературе [1, 2], и ряд упрощенных моделей для вычислительных систем и сетей, изложенных в зарубежной литературе [3]. Однако эти модели, в основном базируются на модели восстанавливаемых элементов и не учитывают специфику систем обработки данных, различную интенсивность отказов в различных режимах работы узлов, конечное время подключения резервного узла.
В такой ситуации возникает необходимость в разработке специализированной модели надежности кластера высокой готовности и выведении расчетных формул для показателей надежности. Соответственно, в рамках научных исследований автора в области надежности систем обработки и передачи данных [4-10] перед автором возникла научная задача разработки специализированной модели надежности системы с основным и резервным узлами обработки данных, для последующего использования полученных результатов при проектировании систем обработки данных для промышленных предприятий.
Упрощенная модель надежности дублированной системы. В упрощенной модели надежности дублированной системы мы рассматриваем узлы обработки данных как простейшие восстанавливаемые элементы с двумя состояниями: работоспособный и неработоспособный (рис. 1). Работоспособный узел отказывает с интенсивностью λA и переходит в неработоспособное состояние. Неработоспособный узел восстанавливается с интенсивностью μN и переходит в работоспособное состояние.
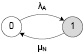
Рис. 1. Граф состояний узла с двумя состояниями
В дублированной системе с независимыми узлами оба узла могут находиться одном из двух состояний независимо друг от друга, и система считается готовой обслуживать запросы пользователей, когда хотя бы один узлов находиться в работоспособном состоянии.
Более того, одни и те же запросы пользователей могут одновременно обрабатываться на обоих узлах, если оба узла работоспособны. Рассмотрим множество состояний системы:
Состояние 0 – оба узла работоспособны и обрабатывают запросы пользователей. Из этого состояния система с интенсивностью 2λA (отказ одного из работоспособных узлов) может перейти в состояние 1.
Состояние 1 – один из узлов работоспособен и обрабатывает запросы пользователей, другой неработоспособен. Из этого состояния система либо с интенсивностью λA (отказ работоспособного узла) может перейти в состояние 2, либо с интенсивностью μN (восстановление неработоспособного узла) перейти в состояние 0.
Состояние 2 – оба узла неработоспособны, и система не обрабатывает запросы пользователей. Из этого состояния система с интенсивностью 2μN (восстановление одного из неработоспособных узлов) может перейти в состояние 1.
Тогда, с учетом вышесказанного имеем следующий граф состояний (рис. 2):
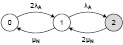
Рис. 2. Упрощенная модель надежности дублированной системы
Математическая модель (система уравнений Колмогорова-Чепмена):
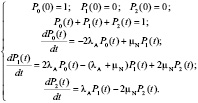
Мы ограничимся выводом аналитического решения для стационарного случая при 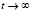 , когда марковский процесс становится установившимся, и производные вероятностей по времени стремятся к нулю. Тогда мы имеем дело с системой алгебраических уравнений, и, решая ее, получаем формулы для стационарных вероятностей всех состояний:
, когда марковский процесс становится установившимся, и производные вероятностей по времени стремятся к нулю. Тогда мы имеем дело с системой алгебраических уравнений, и, решая ее, получаем формулы для стационарных вероятностей всех состояний:
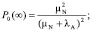
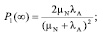
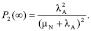
Соответственно, стационарный коэффициент готовности дублированной системы, с учетом того, что в состояниях 0 и 1 система обрабатывает запросы пользователей:
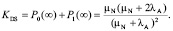 (1)
(1)
Модель системы с основным и резервным узлами. Для учета конечного времени подключения резерва и учета различной интенсивности отказов узлов в нагруженном и ненагруженном режимах в усовершенствованной модели системы будем рассматривать узлы как элементы с тремя состояниями: пассивный, активный и неработоспособный (рис. 3).
Только в активном состоянии узел обрабатывает запросы пользователей. Пассивный узел либо отказывает с интенсивностью λP и переходит в неработоспособное состояние, либо переходит в активное состояние с интенсивностью γN. Активный узел отказывает с интенсивностью λA и переходит в неработоспособное состояние. Неработоспособный узел восстанавливается с интенсивностью μN и переходит в пассивное состояние.
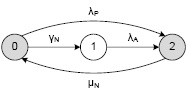
Рис. 3. Граф состояний узла с тремя состояниями
Будем считать, что в системе с одним основным и одним резервным узлом в каждый момент времени только один узел может быть активным (иметь доступ к общей базе данных и обрабатывать запросы пользователей). Соответственно, если оба узла находятся в пассивном состоянии, то только один из них переводится в активное состояние. Что касается отказов и восстановлений узлов, для упрощения модели будем считать, что узлы независимы по отказам и восстановлениям. Рассмотрим множество состояний системы:
Состояние 0 – оба узла работоспособны, но пассивны. Из этого состояния система с интенсивностью γN (активация одного пассивного узла, используемого в качестве основного) может перейти в состояние 1, либо с интенсивностью 2λP (отказ любого из двух пассивных узлов) перейти в состояние 2.
Состояние 1 – оба узла работоспособны, и один из узлов активен, другой – пассивен. Из этого состояния система с интенсивностью λA (отказ активного узла) может перейти в состояние 2, либо с интенсивностью λP (отказ пассивного узла) перейти в состояние 3. В состоянии 1 система может обрабатывать запросы пользователей.
Состояние 2 – один узел неработоспособен, другой работоспособен, но пассивен. Из этого состояния система с интенсивностью γN (активация пассивного узла) может перейти в состояние 3, либо с интенсивностью λP (отказ пассивного узла) перейти в состояние 4, либо с интенсивностью μN (восстановление неработоспособного узла) перейти в состояние 0.
Состояние 3 – один узел неработоспособен, другой работоспособен и активен. Из этого состояния система с интенсивностью λA (отказ активного узла) может перейти в состояние 4, либо с интенсивностью μN (восстановление неработоспособного узла) перейти в состояние 1. В состоянии 3 система может обрабатывать запросы пользователей.
Состояние 4 – оба узла неработоспособны. Из этого состояния система с интенсивностью 2μN (любой из двух неработоспособных узлов может восстановиться) может перейти в состояние 2.
Тогда, с учетом вышесказанного имеем следующий граф состояний (рис. 4):
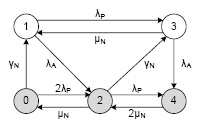
Рис. 4. Модель надежности системы с основным и резервным узлом
Математическая модель (система уравнений Колмогорова-Чепмена):
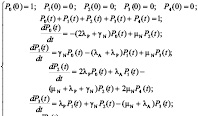
Мы ограничимся выводом аналитического решения для стационарного случая при 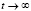 , когда марковский процесс становится установившимся, и производные вероятностей по времени стремятся к нулю. Тогда мы имеем дело с системой алгебраических уравнений, и, решая ее, получаем формулы для стационарных вероятностей всех состояний:
, когда марковский процесс становится установившимся, и производные вероятностей по времени стремятся к нулю. Тогда мы имеем дело с системой алгебраических уравнений, и, решая ее, получаем формулы для стационарных вероятностей всех состояний:
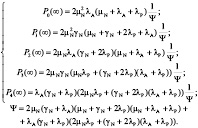
Тогда, с учетом того, что система обрабатывает запросы пользователей только в состояниях 1 и 3, получаем стационарный коэффициент готовности 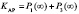 :
:
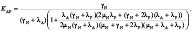 (2)
(2)
Примечание 1. При быстрой активации узлов γN →∞, коэффициент готовности:
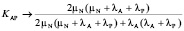 .
.
Если при этом еще интенсивности отказов активного и пассивного узлов совпадают λA=λP, то приходим к упрощенной формуле 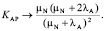
Пример расчета коэффициента готовности
Пусть имеется система с двумя узлами обработки данных. Интенсивность отказов активного узла λA = 1/8760 час-1 (в среднем раз в год). Интенсивность восстановления узла: μN=1/24 час-1 (восстановление в среднем в течение 24 часов).
Что касается интенсивности отказов и интенсивности активации пассивного узла, рассмотрим три случая:
Горячий резерв с быстрой активацией: интенсивность отказов пассивного узла λP=1/8760 час-1, интенсивность активации γN=1200 час-1 (в среднем активация происходит в течение 3 секунд).
Теплый резерв со средней активацией: интенсивность отказов пассивного узла 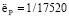 час-1, интенсивность активации γN=20 час-1 (в среднем активация происходит в течение 3 минут).
час-1, интенсивность активации γN=20 час-1 (в среднем активация происходит в течение 3 минут).
Холодный резерв с медленной активацией: интенсивность отказов пассивного узла λP=0 час-1, интенсивность активации γN=1/3 час-1 (в среднем активация происходит в течение 3 часов).
В упрощенной модели для дублированной системы во всех трех случаев по формуле 1 мы получаем коэффициент готовности:
KDS≈0,9999925349
В усовершенствованной модели системы с основным и резервным элементом по формуле 2 мы получаем:
В случае горячего резерва с быстрой активацией:
KAP≈0,9999924397
В случае теплого резерва со средней активацией:
KAP≈0,9999886897
В случае холодного резерва с медленной активацией:
KAP≈09996543268
Нетрудно заметить, что усовершенствованная модель, учитывающая конечное время активации узлов и различные интенсивности отказов в активном и пассивном состояниях, дает более низкую и реалистичную оценку коэффициента готовности системы с основным и резервным узлом, нежели чем известная упрощенная модель.
Заключение
Таким образом, в рамках данной статьи рассмотрена предложенная автором модель надежности системы обработки данных с одним основным и одним резервным узлом. Выведены формулы для расчета коэффициента готовности системы. Также приведен пример расчета коэффициента готовности для различных случаев.
Полученные теоретические результаты использовались в многолетней практике эксплуатации, развития и проектирования систем хранения и обработки данных НИУ МЭИ (ТУ), Балаковской АЭС, ОАО «Красный Пролетарий» и ряда других предприятий.
Библиографическая ссылка
Рахман П.А. КОЭФФИЦИЕНТ ГОТОВНОСТИ СИСТЕМЫ ОБРАБОТКИ ДАННЫХ С ОСНОВНЫМ И РЕЗЕРВНЫМ УЗЛАМИ // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 9-4. – С. 608-611;URL: https://applied-research.ru/ru/article/view?id=7556 (дата обращения: 24.04.2024).

