Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Файлы

Зюкин П.Н. 1 Сапронов И.В. 1 Уточкина Е.О. 1

---

1 ФГБОУ ВО «Воронежский государственный лесотехнический университет им. Г.Ф. Морозова»

Статья в формате PDF

857 KB

Рассматривается задача Коши

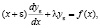(1)

yε(0) = ψ(ε). (2)

где 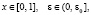l – комплексное число, f(x) – гладкая (то есть бесконечно дифференцируемая на отрезке [0,1]) функция, значениями которой являются комплексные числа. При каждом 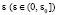решение задачи (1), (2) будем обозначать yε(x). Дифференциальное уравнение, в которое переходит уравнение (1) при 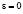, обозначим (3). Пусть y(x) – гладкое решение уравнения (3), k – наименьшее из натуральных чисел n таких, что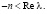

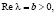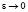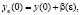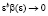Теорема 1. Если то для функций yε(x) явление пограничного слоя по отношению к y(x) в точке x = 0 при имеет место в том и только том случае, если где и 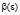не стремится к 0 при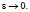

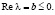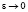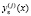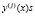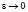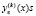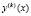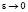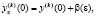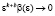Теорема 2. Пусть Тогда для функций yε(x) явление пограничного слоя по отношению к y(x) в точке x = 0 при отсутствует, для функций (j – натуральное число, 1 ≤ j ≤ k – 1) в случае k > 1 явление пограничного слоя по отношению к в точке x = 0 при отсутствует, для функций явление пограничного слоя по отношению к в точке x = 0 при имеет место в том и только том случае, если где и 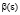не стремится к 0 при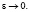

Библиографическая ссылка