В последние годы растет интерес к нелинейным явлениям в магнетиках и мультиферроиках со спиральной (полосовой доменной) структурой. Спиральная структура представляет собой сильно нелинейное неоднородное основное состояние среды, которое теоретически описываются одномерной решеткой солитонов (решеткой 2π-кинков). При описании магнетиков и мультиферроиков с геликоидальной или циклоидальной спиновой структурой наиболее популярна модель sine-Gordon:
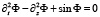. (1)
Угол Ф характеризует распределение вектора ферро- или антиферромагнетизма. Например, в ферромагнетике без центра инверсии с анизотропией типа «легкая плоскость» (соединение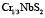 
) вектор ферромагнетизма 
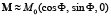, где M0 – номинальная намагниченность.
В безразмерных переменных плотность энергии магнетика с модулированной структурой принимает вид [3-5]:
.
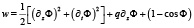Управляющий параметр q зависит от температуры или внешнего поля (электрического или магнитного). В зависимости от величины q, минимуму энергии отвечает либо однородное распределение параметра порядка Ф = 0 (mod 2π), либо спиральная структура, которая описывается эллиптической амплитудой Якоби: Ф = φ0(z) = π – 2am(χ, k) с модулем k (k2 ≤ 1), где χ = z/k (рис. 1). На периоде L0 = 2Kk функция φ0(z) изменяется на 2π. Ее изменения сосредоточены в узкой области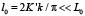 
, где 
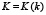и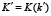 
– полные эллиптические интегралы первого рода; 
.
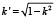В [3-5] сформулирована модификация метода обратной задачи рассеяния, пригодная для полного исследования солитонов и волн в спиральной структуре при локализованных начальных возмущениях и заданных граничных условиях на бесконечности. В данной работе результаты работ [3-5] дополнены подробным анализом особенностей пульсирующих солитонов – бризеров. Детальное исследование строения солитонов позволяет предложить способы их возбуждения в спиральной структуре магнетиков без центра инверсии.
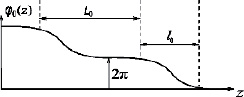
Рис. 1. Основное состояние магнетика со спиральной структурой
Бризер в спиральной структуре. Аналитическое решение для бризера на фоне структуры имеет вид [3-5]:
, 
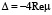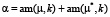; (2)
;
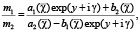
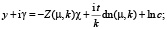
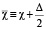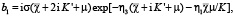
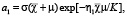
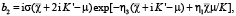
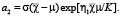
Здесь c – комплексная постоянная интегрирования, Z(u, k) – зета-функция Якоби, dn(μ, k) – эллиптическая функция Якоби,σ(u) и ζ(u) – сигма- и дзета-функции Вейерштрасса с периодами 2K,4iK’; η1 = ζ(K), η3 = (2iK’) [1-2].
Образование бризера сопровождается макроскопическим фазовый сдвигом структуры 0 < kΔ < 2L0, который явно входит в краевые условия задачи:
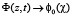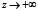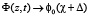при 
;
при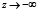 
. (3)
Комплексный параметр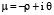 
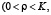
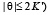определяет скорость бризера 
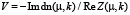, ширину ограничивающих его доменных стенок, а также волновое число 
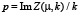и частоту 
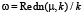пульсаций поля Ф в области локализации бризера. Предельная скорость бризера не превышает максимальной групповой скорости активационных спиновых волн на фоне структуры [8], которая в безразмерных переменных равна единице.
Поскольку первый член решения (2) не зависит от времени, амплитуда пульсаций бризера определяется вторым слагаемым. Ввиду того, что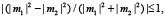 
это слагаемое по величине не превышает 
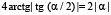. Для неподвижного бризера параметр θ = 0. Детальный анализ показывает, что амплитуда неподвижного бризера в точности равна 
.
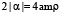Неподвижный бризер наиболее удобен для наблюдения. При 0 < ρ ≤ 0,2K он представляет собой протяженную область малоамплитудных колебаний поля Ф около равновесных положений слабодеформированной структуры. При 0,2K < ρ < K колебания бризера локализуются в конечной области – в его ядре. Центр бризера сдвигается вдоль спиральной структуры при изменении параметра ln|c|. Нагляднее всего случай, когда область интенсивных колебаний попадает внутрь одного из доменов структуры (рис. 2). На рис. 2 сплошной, штриховой и пунктирной линиями отмечены положения бризера в различные моменты времени. В асимптотике при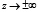 
бризер выходит на фоновую структуру (3), изображенную штрих-пунктиром.
Взаимодействие ядра бризера со структурой оказывается важным и проявляется в новых свойствах всей системы. Прежде всего ядро бризера отодвигает от себя ближайшие кинки спиральной структуры. Так при ρ = K/2 оно колеблется в пределах домена, длина которого в терминах χ = z/k больше периода 2K спиральной структуры и составляет величину порядка 3K. Именно в этом кроется причина сдвига Δ в краевых условиях (3) задачи при образовании бризера в решетке кинков. Сдвиг Δ связан с параметром ρ соотношением: Δ = 4ρ.
В отличие от бризера на однородном фоне, ядро бризера в структуре не только пульсирует, но и совершает дополнительные малые колебания между стенками протяженного домена. Протяженный домен играет роль резонатора. Половинки ядра бризера по-разному деформируются в ходе колебаний центра бризера вдоль такого резонатора. Продольные колебания ядра бризера передаются ближайшим к нему кинкам структуры.
На больших расстояниях от ядра поле Ф неподвижного бризера имеет узлы, расположенные в точках:
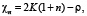
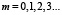
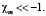
Доменные стенки располагаются между узлами (жирные точки на рис. 2). Все четные (нечетные) стенки структуры колеблются в фазе по отношению друг к другу и в противофазе по отношению к нечетным (четным) стенкам, что отражено выбором направлений стрелок на рис. 2. Числа в кружочке нумеруют доменные стенки. Ядро бризера колеблется между узловыми точками χ = – 3ρ и χ = 2K – ρ. В некоторые моменты времени ядро принимает форму «плато» протяженностью 2K + 2ρ. Плато образует с осью Оx малый угол J: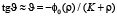 
. Ближайшие к ядру стенки (с номером n = 1) колеблются в противофазе с ядром. Колебания последующих стенок (с номерами n = 2,3…) экспоненциально убывают с ростом их номера. Частота колебаний стенок равна частоте бризера.
Для соединения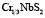 
зависимость периода спиральной структуры L0 от модуля k (управляющего параметра q) хорошо описывается моделью sine-Gordon [10]. Примем за материальные параметры этого соединения значения, использованные в работах [6, 10]. Тогда при 0,2K ≤ ρ ≤K для частоты пульсаций бризера получим оценку v∞107 – 108 Гц. Отсюда следует, что бризер в спиральной структуре можно обнаружить по поглощению СВЧ-мощности на характерных частотах его пульсаций. Эти частоты попадают в энергетическую щель спектра активационных и голдстоуновских стоячих линейных волн на фоне структуры.
В общем случае движущегося бризера, его структура как целого существенно зависит от соотношения поступательной скорости бризера V и фазовой скорости Vph = ω/p волновых процессов в его ядре. При V < Vph деформации спиральной структуры подстраиваются к пульсациям бризера. В ходе движения ядра бризера пульсации его поля «перетекают» из одного домена структуры в соседний подобно тому, как это происходит при сближении бризера с отдельной доменной стенкой на однородном фоне [3]. При V > Vph, напротив, деформации фоновой структуры отстают от изменения ядра бризера (см. рис. 3). При этом происходит следующее. Вначале движение ядра немного замедляется деформацией структуры на переднем фронте бризера. В некоторый момент времени центр ядра бризера достигает предельного значения (точка A), после чего левый край ядра (точка B) «отрывается» от фоновой структуры. Начиная с этого момента, левый край бризера ведет себя как центр нового ядра, в то время как центр прежнего ядра становится краем доменной стенки. Новый центр ядра немного замедляется. Поэтому на рис. 3 он начинает «подниматься» вверх по ступенькам структуры. В результате перед ядром образуется «предвестник» бризера в виде деформаций спиральной структуры. Ядро бризера «поднимается» до максимального уровня B’, а затем начинает наращивать свою скорость, вследствие чего «предвестник» сокращается и в некоторый момент исчезает. Тогда весь бризер оказывается локализованным в пределах своего ядра. Однако далее бризер по инерции «проскакивает» это состояние и, двигаясь с замедлением, оставляет после себя квазистатический «хвост». Иными словами, при V > Vph поступательное движение ядра бризера сопровождается его колебаниями вдоль структуры с поочередным образованием «предвестников» и »хвостов» из ее квазистатических деформаций.
В мультиферроиках спиральное магнитное упорядочение сопровождается образованием решетки солитонов электрической поляризации. Они модулируют диэлектрическую проницаемость среды. Поэтому деформации спиральной структуры при возбуждении в ней солитонов можно визуализировать не только магнитооптическими, но и оптическими методами. Кроме того, бризер в мультиферроике можно обнаружить путем фиксации локальных электрических полей от его ядра. При движении ядра содержащий его удлинненный домен перемещается по структуре со скоростью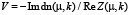 
.
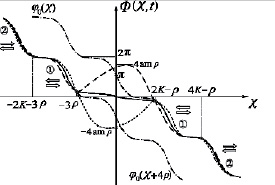
Рис. 2. Неподвижный бризер на фоне спиральной структуры в случае, когда его центр совпадает с серединой одного из доменов
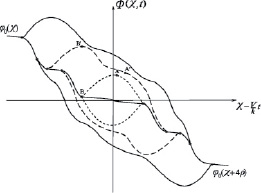
Рис. 3. «Хвосты» и »предвестники» движущегося бризера
Возбуждение бризера в спиральной структуре. Проведенный анализ подсказывает пути возбуждения бризера в спиральной структуре. Необходимо посредством внешних полей удлинить и возмутить один из доменов структуры так, чтобы он стал резонатором для бризера. Это можно сделать посредством модуляций внешнего поля.
Данные соображения можно подтвердить расчетом. Зададим начальное возмущение спиральной структуры в виде ступеньки шириной d и высотой 2f:
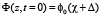при 
,
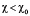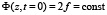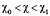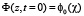при 
,
при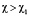 
,
где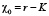 
, 
, 
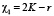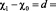
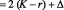. Согласно [7, 9], начальные возмущения могут генерировать бризер только при условии
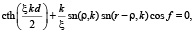
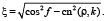(4)
Здесь sn(ρ, k), cn(ρ, k) – эллиптические функции Якоби с модулем k. Величина K – r(0 ≤ r ≤ K) определяет смещение ступеньки относительно структуры. При r = K ступенька моделирует начальное возмущение одного из доменов структуры длиной d = Δ. Согласно численному моделированию, такая ступенька порождает бризер, начиная с пороговых значений ее высоты 2f ≥ 3am(ρ,k). В случае 4am(ρ,k) <2f ≥ 6am(ρ,k) начальное возмущение сначала снижает амплитуду до уровня A = 4am(ρ,k), сбрасывая избыток энергии в виде диспергирующих волн. Затем из него формируется неподвижный бризер, ядро которого располагается в середине резонаторного домена. Когда высота ступеньки 2f ≥ 6am(ρ,k), она распадается на два бризера, движущихся в противоположных направлениях.
Аналитический расчет (4) дает близкие результаты. А именно, если задать ступеньку высоты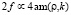 
, то уравнение (4) имеет решения, когда параметр ρ лежит в интервале 1,8K ≤ ρ ≤ 2,5K. При этом Δ = 4ρ = d. Мы полагаем, что эти результаты можно использовать для планирования экспериментов по обнаружению бризерных возбуждений в магнетиках и мультиферроиках со спиральной или циклоидальной спиновой структурой.
Авторы выражают благодарность С.В. Баталову за помощь в проведении численных расчетов.
Работа выполнена в рамках проекта УрО РАН №15-8-2-7 «Локализованные структуры, солитоны и их возбуждение в конденсированных средах».
Библиографическая ссылка
Киселев В.В., Расковалов А.А. СОЛИТОНЫ В СПИРАЛЬНОЙ МАГНИТНОЙ СТРУКТУРЕ И СПОСОБЫ ИХ ВОЗБУЖДЕНИЯ // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 12-1. – С. 42-46;URL: https://applied-research.ru/ru/article/view?id=7811 (дата обращения: 24.04.2024).