Существенный интерес в динамике машин представляют методы синтеза движений, обеспечивающих устойчивость системы, как в точке, так и на замкнутых траекториях различного вида.
Задача управляемости линейной системы в точке в смысле перевода ее из произвольного положения в нулевое решается в известной теореме Калмана об управляемости. Для нелинейных задач универсальных методов синтеза и анализа нелинейных систем не существует.
Cоздание методов синтеза управляемых режимов, обеспечивающих устойчивое движение по замкнутым траекториям с участками, близкими к прямолинейным, для многомерных систем является актуальным.
Рассмотрим математическую модель динамической системы, движение которой описывается уравнениями объекта управления, уравнениями генератора асимптотически устойчивых траекторий с участками, близкими к прямолинейным, и уравнениями связей.
Уравнения объекта управления имеют форму дифференциально-алгебраических уравнений [1]. Такая форма уравнений позволяет рассматривать динамику объектов различного вида – механических, электромеханических, гидромеханических и т.д. Для управляемых машин (роботов, манипуляторов) запись уравнения движения в данной форме позволяет решать задачу синтеза управляемого движения многомерных пространственных механических систем [4]. При решении задачи синтеза задается функция, описывающая программное движение отдельных точек системы. Для улучшения качества управления необходима разработка методов, в которых такая функция обладает следующими свойствами: является 1) аналитической в пространстве состояний системы, 2) была бы близка к программной траектории и 3) асимптотически устойчивой.
Движение некоторых точек механической системы произвольной структуры по заданным траекториям можно записать в виде системы уравнений вида
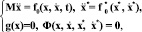
где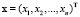 
– вектор обобщенных координат управляемой системы (объекта управления), 
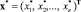– вектор обобщенных координат генератора системы, М – матрица инерции объекта управления, векторы 
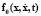– внутренних сил объекта управления, 
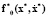– правых частей генератора заданных траекторий, g(x) – геометрических связей внутри объекта управления, .. – связей между генератором и объектом управления (в общем случае неголономных, неинтегрируемых связей).
С учетом множителей Лагранжа и после двукратного дифференцирования уравнений связи, что необходимо для численного интегрирования, систему можно записать в виде
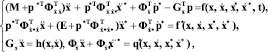
где матрицы Gx – переменных коэффициентов связей внутри объекта управления,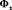 
, 
, 
, 
, 
, 
, 
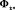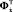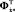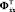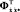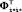– переменных коэффициентов при множителях Лагранжа и их производных, векторы 
, 
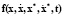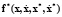– правых частей уравнения объекта управления и уравнения генератора; 
, 
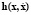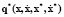– правых частей уравнений связей, p – множителей Лагранжа, соответствующий связям внутри объекта управления, p* – множителей Лагранжа, соответствующий связям между объектом управления и генератором траекторий.
Уравнения генератора программной траектории и уравнения связей могут иметь различный вид. В зависимости от этого можно выделить несколько случаев задания управляемого движения. Рассмотрим эти случаи.
1. Уравнения генератора записываются в виде дифференциальных уравнений второго порядка, и программная траектория определяется решением этих уравнений. В этом случае уравнения управляемой системы имеют вид
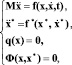(1)
g(x),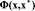 
– векторы связей. Уравнения связей для этого случая задаются в виде равенства соответствующих координат (голономные связи). Для замыкания уравнений системы (1) введем множители Лагранжа с помощью соответствующих уравнений Эйлера для условия экстремума функционала, тогда система (1) запишется в виде
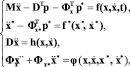(2)
где p* – вектор множителей Лагранжа, соответствующих связям с заданными программными траекториями;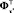 
– матрицы переменных коэффициентов связей точек; 
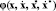– вектор правых частей уравнений связей после двукратного дифференцирования.
В качестве примера можно рассмотреть систему, где масса m принуждается двигаться по траектории, задаваемой гармоническим осциллятором. Уравнения (1) будут иметь вид
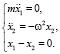(3)
А уравнения (2) –
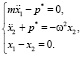(4)
Такие системы обычно решаются с помощью двукратного дифференцирования уравнения связи [1]. После чего ее можно разрешить относительно старших производных и множителя Лагранжа:
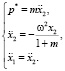(5)
При любых значениях m ≠ 0 управляемое движения x1 будет отличаться от программного движения x2. Указанного несоответствия можно избежать, умножив обе части второго уравнения системы (3) на некоторый параметр α.
Тогда система (5) примет вид
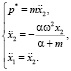
Очевидно, при достаточно больших значениях величины α решение уравнения будет стремиться к заданной траектории: координата x1 стремится к координате x2.
Уравнения генератора замкнутых траекторий сложной формы в виде второго уравнения системы (1) выписать сложно. В работах [2, 3] были описаны генераторы автоколебаний в форме дифференциальных уравнений первого порядка. Рассмотрим возможность включения в управляемую систему таких уравнений генераторов.
2. Для согласования уравнений связей, т.е. чтобы уравнения связей оставались голономными или интегрируемыми неголономными, целесообразно генератор записывать в виде
.
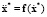Для указанного типа связей задание траекторий генератора в форме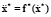 
обеспечивает непрерывность функций, описывающих программную траекторию движения. Тогда уравнения связей с объектом управления можно представить
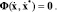
В этом случае уравнения управляемой системы будут иметь вид
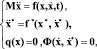(6)
Уравнения Эйлера для системы (6) запишутся в виде
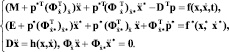(7)
В частности, примером системы (6) в случае движения массы m по заданной траектории является система
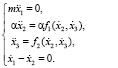(8)
где
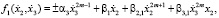
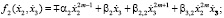(9)
коэффициенты при переменных в (9) удовлетворяют соотношениям, полученным в работе [2]; а для системы (7) –
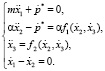(10)
Для сложных траекторий (9) предложенный в работе [2, 3] метод синтеза обеспечит непрерывность функций, описывающих программную траекторию, и асимптотическую устойчивость движения точки по заданному предельному циклу.
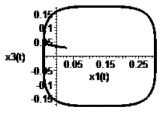
Рис. 1. Предельный цикл при α = 1
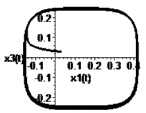
Рис. 2. Предельный цикл при α = 100
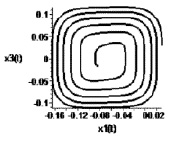
Рис. 3. Стабилизация в точку при α = 1
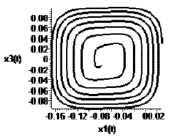
Рис. 4. Стабилизация в точку при α = 100
Разрешив относительно старших производных и множителя Лагранжа систему (10), получим
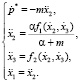
На рис. 1–4 представлены устойчивые предельные циклы и стабилизация в точку системы управления в подпространстве X1X3 в случае различных значений параметра α.
При увеличении α интегральная кривая выходит на заданный устойчивый режим; скорость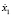 
стремится к скорости 
.
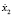Таким образом, разработанная методика сопряжения дифференциальных уравнений генераторов нелинейных колебаний с дифференциально-алгебраическими уравнениями объекта управления позволяет реализовывать автоколебательные режимы движения звеньев объекта управления по замкнутым траекториям с участками, близкими к прямолинейным.
Библиографическая ссылка
Полянина А.С. ЗАДАЧА СИНТЕЗА АВТОКОЛЕБАТЕЛЬНЫХ РЕЖИМОВ В МНОГОМЕРНЫХ ДИНАМИЧЕСКИХ СИСТЕМАХ // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 12-4. – С. 618-621;URL: https://applied-research.ru/ru/article/view?id=7989 (дата обращения: 16.04.2024).