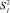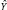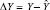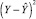Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Беззубцева М.М. 1 Волков В.С. 1

---

1 ФГБОУ ВПО «Санкт-Петербургский государственный аграрный университет»

В статье представлены результаты прикладных исследований электромагнитного способа механоактивации на примере диспергирования шоколадных масс. Приведена экспериментально-статистическая модель процесса диспергирования рецептурной смеси сахара и какао электромагнитным способом на электромагнитном механоактиваторе (ЭММА), представляющим предмет изобретения. Анализ модели подтвердил теоретические исследования, положенные в основу формирования энергоэффективного способа активации. Приведены результаты оптимизации, позволяющие выявить режимы работы устройства, при которых достигается оптимальное силовое воздействие и стандартизованная величина степени измельчения шоколадной массы с высокой однородностью ее гранулометрического состава.

Статья в формате PDF

352 KB

электромагнитные механоактиваторы

шоколадная масса

математическая модель

1. Беззубцева М.М., Волков В.С. Теоретические исследования электромагнитного способа измельчения материалов (монография) // Международный журнал экспериментального образования. – 2015. – № 2–1. – С. 68–69.

2. Беззубцева М.М., Обухов К.Н.К вопросу исследования физико-механических процессов в магнитоожиженном слое ферротел // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 7–2. – С. 191–195.

3. Беззубцева М.М., Обухов К.Н. Энергетические параметры, характеризующие работу электромагнитных механоактиваторов // Международный журнал экспериментального образования. – 2015. – № 8–1. – С. 134–135.

4. Беззубцева М.М., Волков В.С., Котов А.В., Обухов К.Н. Инновационные электротехнологий в АПК (учебное пособие) // Международный журнал экспериментального образования. – 2015. – № 2–2. – С. 221.

5. Беззубцева М.М., Волков В.С. Классификация электромагнитных механоактиваторов по технологическому назначению // Международный журнал экспериментального образования. – 2015. – № 8–1. С. 25–27.

6. Беззубцева М.М., Волков В.С. Исследование закономерностей электромагнитной механоактивации в дисковом электромагнитном механоактиваторе (ЭДМА) // Научное обеспечение развития АПК в условиях реформирования: сборник научных трудов по материалам Международной научно-практической конференции профессорско-преподавательского состава. Министерство сельского хозяйства Российской Федерации. – СПб.: Санкт-Петербургский государственный аграрный университет, 2014. – С. 286–288.

7. Беззубцева М.М., Волков В.С.К вопросу исследования энергоэффективности механоактиваторов с магнитоожиженным слоем // Современные проблемы науки и образования. – 2015. – № 2. – С. 248.

8. Беззубцева М.М., Волков В.С.Теоретические исследования электромагнитного способа измельчения материалов (монография) // Международный журнал экспериментального образования. – 2015. – № 2–1. – С. 68–69.

9. Беззубцева М.М., Обухов К.Н. К вопросу исследования физико-механических процессов в магнитоожиженном слое ферротел // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 7–2. – С. 191–195.

10. Беззубцева М.М., Обухов К.Н. К вопросу исследования диспергирующих нагрузок в электромагнитных механоактиваторах // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 8–5. – С. 847–851.

11. Беззубцева М.М., Волков В.С. К расчету энергоэффективных режимов работы механоактиваторов // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 9–1. – С. 9–13.

12. Беззубцева М.М., Обухов К.Н. Электромагнитный способ снижения энергоемкости продукции на стадии измельчения // Международный журнал экспериментального образования. – 2015. – № 8–3. – С. 399–400.

13. Беззубцева М.М., Волков В.С., Котов А.В., Обухов К.Н. К вопросу исследования зависимости технологического эффекта измельчения рецептурных компонентов шоколадного производства от режимов работы электромагнитных механоактиваторов // Современные проблемы науки и образования. – 2015. – № 1. – С. 358.

14. Беззубцева М.М., Волков В.С., Обухов К.Н. Электромагнитная механоактивация полуфабрикатов шоколадного производства // Международный журнал экспериментального образования. – 2015. – № 3–1. – С. 73–74.

15. Беззубцева М.М., Волков В.С., Котов A.B., Обухов К.Н. К вопросу исследования электромагнитного способа механоактивации рецептурных компонентов шоколадных изделий // Современные наукоемкие технологии. – 2015. – № 4. – С. 12–14.

16. Беззубцева М.М. Теоретические основы электромагнитного измельчения. ? СПб.: СПбГАУ, 2005. – 154 с.

Наиболее полное математическое описание процессов измельчения твердых тел осуществляется в настоящее время методом экспериментально-статистических исследований. Ценность экспериментально-статистических моделей процесса, полученных на основе этого метода, заключается в том, что они, во-первых, дают информацию о влиянии факторов; во-вторых, позволяют количественно определить значения функций отклика при заданных режимах работы ведения процесса; и, в-третьих, могут служить основой для оптимизации. Целью математического описания процесса диспергирования рецептурной смеси сахара и какао электромагнитным способом являлось построение интерполяционной формулы, подтверждающей теоретические положения способа создания диспергирующего усилия с применением постоянного по знаку и регулируемого по величине электромагнитного поля [1, 2, 3, 4, 5].

Целью исследования является подтверждение теоретических исследований, положенных в основу формирования электромагнитного способа механоактивации (на примере измельчения рецептурных смесей шоколадных масс).

Материалы и методы исследований

Режимы работы электромагнитных механоактиваторов (ЭММА), при которых достигается оптимальное силовое взаимодействие между ферроэлементами в магнитоожиженном слое, обеспечивающее стандартизованную степень измельчения шоколадной массы с высокой однородностью гранулометрического состава ее твердой фазы. Использованы экспериментально-статистические методы исследования.

Результаты исследования и их обсуждение

Для описания исследуемого процесса была применена линейная модель – алгебраический полином 1-й степени

Y = b0 + b1 X1 + b2 X2…bi Xi, (1)

где Y – выходной параметр процесса, в данном случае степеньизмельчения шоколадных масс, %; X1, Х2, … Хi – независимые переменные, факторы,определяющие ход процесса.

Определение коэффициентов полинома (1) производится в результате факторного эксперимента, сущность которого состоит в одновременном варьировании определяющих факторов по разработанному плану.

Опыт работы кондитерских предприятий, результаты научных исследований, а также проведенные эксперименты показали [6, 7, 8, 9], что на процесс измельчения шоколадных масс может оказывать влияние большое количество факторов механического и технологического характера. Наличие большого количества управляемых факторов усложняет получение основных закономерностей изучаемого процесса и требует критического подхода к исследованию их влияния на процесс диспергирования в ЭММА. Выбор существенных факторов при математическом моделировании определяется постановкой задачи, условиями проведения эксперимента, а также состоянием теоретических предпосылок в этой области [10, 11]. Анализ влияющих факторов показал, что часть из них принимается строго определенной, исходя из конструктивнотехнологических соображений и на основании предварительной информации [12]. Фиксированными механическими факторами являются: материал и размер рабочей камеры, форма, размер и материал мелющих тел, коэффициент заполнения рабочего объема обрабатываемым продуктом [13]. В качестве фиксированых технологических факторов установлены: соотношение рецептурных компонентов, содержание жира, начальный размер частиц смеси [14].

Представление о роли различных факторов, а также оценки «силы их влияния», полученной на основании предварительных экспериментов, позволили выделить три основных фактора, влияющих на процесс диспергирования шоколадных масс в ЭММА: индукция в рабочем объеме В0, частота вращения внутреннего цилиндра n, коэффициент заполнения рабочего объема мелющими телами Kрэ. Таким образом, необходимо исследовать зависимость

Dδφ30 = φ(B, n, Kрэ). (2)

Априори определенное факторное пространство представлено в табл. 1. Матрица планирования и результаты экспериментов на этих уровнях представлены в табл. 2.

Опыты были дублированы и рандомизированы во времени. По результатам полного факторного эксперимента рассчитаны коэффициентырегрессии и получено следующее уравнение регрессии:

Y = 93 + 1,687X1 + 1,187X2 + 3,06X3 + 0,3125X12 – 0,3125X13 – 0,1878X23 – 0,1875X123. (3)

Таблица 1

Факторное пространство

Максимальная из рассчитанных построчных дисперсий 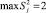; сумма всех дисперсий по N строкам матрицы планирования 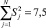; критерий Кохрена GP = 2/7,5 = 0,26. Экспериментальная величина GP критерия не превышает табличного значения GT = 0,68 (для степеней свободы ƒ1 = 1, общего количества оценок дисперсий ƒ2 = 8 и уровня значимости р = 0,05), а следовательно гипотеза об однородности дисперсий принимается.

Таблица 2

Матрица планирования и результаты экспериментов

Таблица 3

Результаты расчета построчных дисперсий

Проверка значимости коэффициентов производилась для каждого коэффициента сравниванием его абсолютного значения bi и доверительного интервала .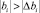

Доверительный интервал Δbi определялся по формуле Δbi = ±tTSbi, (здесь tT – табличное значение критерия Стьюдента, определяемое по числу степеней свободы ƒo для уровня значимости р = 0,05; Sbi – среднеквадратичное отклонение bi). Величина tT критерия равна 2,31 для р = 0,05 и f0 = 8, дисперсия 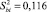. Тогда доверительный интервал Δbi = 0,34·2,31 = 0,785. Абсолютные величины коэффициентов регрессии b1, b2 и b3 больше доверительного интервала, следовательно, гипотеза о незначимости этих коэффициентов отвергается. Коэффициенты регрессии b12, b13, b23, b123 незначимы и соответствующие им члены можно исключить из уравнения регрессии.

Результаты расчета остаточной суммы квадратов при проверке адекватности линейной модели

Y = 93 + 1,687X1 + 1,187X2 + 3,06X3 (4)

приведены в табл. 4.

Таблица 4

Результаты расчета остаточной суммы квадратов

Уравнение регрессии считается адекватным, если выполняется условие Fp < FT (здесь Fp и FT – соответственно расчетное и табличное значения критерия Фишера). Дисперсия адекватности 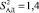, критерий Фишера Fp = 1,5. Табличное значение критерия Фишера для чисел степеней свободы ƒАД = 4 и ƒ0 = 8 равно 3,84. Таким образом, экспериментальная величина Fp критерия не превышает табличного значения и гипотеза об адекватности модели принимается.

Интерпретация полученных результатов заключается в установлении «силы и направления влияния» управляющих факторов, а также в проверке правильности представлений, положенных в основу электромагнитного способа создания измельчающего усилия. Величина коэффициентов регрессии является количественной мерой «силы влияния» факторов, а о характере их влияния говорят знаки коэффициентов. Анализируя полученное уравнение регрессии, можно сделать вывод, что наибольшее влияние на процесс измельчения шоколадных масс на ЭММА оказывает фактор Х3 (коэффициент заполнения рабочего объема мелющими телами), в меньшей мере, но также значительно влияет фактор Х2 (индукция в рабочем объеме) и фактор X1 (частота вращения внутреннего цилиндра). Знак плюс при коэффициентах линейной регрессии свидетельствует, что с увеличением значения факторов растет величина параметра оптимизации, т.е. степень измельчения шоколадных масс увеличивается и процесс диспергирования интенсифицируется. Таким образом, интерпретация полученного уравнения регрессии подтвердила предпосылки, положенные в основу создания измельчающего усилия, реализованного в ЭММА. Экспериментально-статистическая математическая модель процесса диспергирования шоколадных масс на ЭММА, представленная в виде адекватного линейного полинома использовалась для поиска области оптимума объекта исследования. Оптимизация процесса измельчения осуществлялась методом крутого восхождения.

При анализе качества и экономичности приготовления полуфабрикатов шоколадного производства наряду с дисперсностью важным показателем является однородность смеси. Поэтому в качестве ограничивающего параметра была введена в рассмотрение экспериментально найденная функция отклика Yσ, характеризующая однородность смеси σ. Расчет крутого восхождения и полученные результаты приведены в табл. 5. Здесь 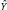и Y – соответственно расчетные и экспериментальные значения степени измельчения полуфабриката. Шаги движения и координаты опытов крутого восхождения в кодированных переменных рассчитывались по формуле

Xi = (xi – x0i)/Гi

(здесь Хi – кодированное значение фактора; xi – натуральное значение фактора; x0i – натуральное значение основного уровня; Гi – интервал варьирования) с использованием физических переменных x1, x2, x3 и шагов варьирования Г1, Г2, Г3, принятых ранее в полном факторном эксперименте. Установлено, что в опыте № 10 достигается граница области определения фактора x3. В данном случае, согласно рекомендациям, был выбран вариант стабилизации этого фактора на данном уровне и дальнейшее продвижение по градиенту по остальным факторам.

Таблица 5

Оптимизация процесса методом крутого восхождения

Анализ полученных данных показал, что в опыте № 13 на граничной области определения по факторам X1 и X2 достигнута максимальная дисперсность смеси, однако однородность смеси значительно хуже, чем в опыте № 10. В условиях опыта № 10 достигается оптимальное соотношение между однородностью σ = 1,55 и максимально возможностей степенью измельчения смеси Dδ30 = 97,2 %. В этой связи оптимальным режимом проведения процесса измельчения шоколадных масс на ЭММА следует считать условия опыта № 10. Для данных режимов работы величина силового взаимодействия между размольными элементами в структурных группах составляет 56,3 Н [16].

Заключение

В результате оптимизации экспериментально-статической модели процесса измельчения шоколадных масс электромагнитным способом определены следующие значения режимных и силовых параметров работы ЭММА, при которых процесс диспергирования протекают с наибольшим эффектом: электромагнитный режим B = 0,37 Тл, скоростной режим n = 23,4 с–1, коэффициент заполнения рабочей камеры размольными элементами Kрэ = 0,35, величина диспергирующего усилия Fr = 56,3 Н. При этом достигается максимальная стандартизованная степень измельчения полуфабриката Dδ30 = 97,2 % и высокая однородность его гранулометрического состава σ = 1,55. Доля фракций размером от 10 до 30 мкм составляет 65 %, что в 2 раза больше по сравнению с продуктом помола, полученным классическим способом, предварительного и тонкого диспергирования рецептурных смесей шоколадных масс на традиционном измельчающем оборудовании.

Библиографическая ссылка