Любое статистическое исследование требует представить первоначально полученную информацию в наглядном виде, удобном для проведения различного рода научных и практических выводов. Статистические данные обрабатываются для получения так называемых вариационных рядов (дискретных или интервальных), дающих наглядное представление о статистическом распределении признака, делающих возможным проведение различного рода исследований. Если изучаемый признак принимает значения, как угодно мало отличающиеся друг от друга, строится интервальный вариационный ряд по частоте. Для построения такого ряда разбивают промежуток, на котором находятся все значения признака, на ряд частичных интервалов и подсчитывают частоту попадания значений признака в каждый частичный интервал. Полученную упорядоченную совокупность интервалов значений признака с соответствующими частотами попадания в каждый из них значений признака и называют интервальным вариационным рядом по частоте.
Вариационные ряды являются составной частью метода статистических оценок результатов наблюдений. Построенный по результатам обработки статистических данных вариационный ряд обрабатывается для получения числовых характеристик изучаемого признака с целью получения научных и практических выводов. Построенные вариационные ряды изображаются графически для получения наглядных представлений о статистическом распределении и анализа информации. Для вариационных рядов также вычисляются основные числовые характеристики: средняя арифметическая, размах вариации, дисперсия, и т.д., с помощью которых становится возможным научное прогнозирование, как важный результат статистического исследования.
Практическая часть исследования включала в себя статистическую обработку признака «балл ЕГЭ по математике», представленных в табл. 1, отображающей данные абитуриентов факультета информатики ФБГОУ ВПО ШГПИ в 2014 г. В качестве источника статистических данных использованы документы архива и бухгалтерии ШГПИ. При работе с табличными данными использовался персональный компьютер конфигурации: процессор Intel Pentium(R) CPU 2,8 Ghz, 4,00 Гб ОЗУ, система Microsoft Windows 7 Professional Service Pack 1, табличный процессор Excel пакета Microsoft Office 2007.
Для изучения признака Х «балл ЕГЭ по математике» извлечена выборка объема 435 (табл. 1).
Таблица 1
|
32 |
48 |
20 |
40 |
56 |
56 |
52 |
32 |
48 |
64 |
52 |
32 |
40 |
48 |
36 |
46 |
32 |
|
52 |
38 |
48 |
32 |
40 |
40 |
44 |
44 |
40 |
36 |
60 |
52 |
75 |
32 |
40 |
46 |
32 |
|
40 |
48 |
36 |
36 |
44 |
48 |
40 |
36 |
48 |
36 |
64 |
44 |
44 |
32 |
36 |
46 |
32 |
|
52 |
32 |
40 |
36 |
44 |
32 |
44 |
68 |
52 |
52 |
44 |
36 |
44 |
44 |
40 |
46 |
32 |
|
36 |
56 |
60 |
44 |
44 |
44 |
44 |
56 |
56 |
48 |
48 |
44 |
36 |
44 |
44 |
46 |
32 |
|
60 |
32 |
44 |
52 |
36 |
36 |
44 |
44 |
77 |
44 |
40 |
32 |
32 |
32 |
32 |
46 |
32 |
|
48 |
44 |
32 |
36 |
52 |
32 |
64 |
44 |
36 |
60 |
56 |
56 |
40 |
40 |
44 |
46 |
32 |
|
48 |
13 |
32 |
40 |
36 |
52 |
48 |
40 |
36 |
64 |
68 |
68 |
36 |
48 |
48 |
46 |
32 |
|
32 |
40 |
52 |
44 |
64 |
44 |
44 |
36 |
44 |
72 |
72 |
52 |
56 |
48 |
36 |
46 |
32 |
|
68 |
44 |
40 |
36 |
36 |
40 |
44 |
40 |
32 |
64 |
56 |
44 |
36 |
32 |
40 |
46 |
32 |
|
32 |
40 |
28 |
40 |
40 |
68 |
32 |
40 |
48 |
44 |
52 |
36 |
48 |
40 |
44 |
46 |
32 |
|
36 |
0 |
52 |
40 |
36 |
48 |
56 |
32 |
48 |
60 |
48 |
36 |
44 |
60 |
40 |
46 |
32 |
|
40 |
56 |
64 |
44 |
48 |
0 |
40 |
40 |
32 |
44 |
36 |
56 |
60 |
48 |
36 |
46 |
32 |
|
32 |
44 |
52 |
60 |
32 |
36 |
40 |
40 |
48 |
44 |
44 |
79 |
48 |
40 |
44 |
46 |
32 |
|
56 |
32 |
44 |
40 |
36 |
48 |
36 |
40 |
40 |
32 |
60 |
60 |
56 |
40 |
40 |
46 |
32 |
|
32 |
48 |
32 |
64 |
64 |
32 |
48 |
48 |
72 |
56 |
44 |
32 |
48 |
56 |
36 |
40 |
44 |
|
44 |
48 |
44 |
48 |
40 |
32 |
40 |
40 |
40 |
36 |
36 |
48 |
52 |
68 |
48 |
40 |
44 |
|
64 |
32 |
36 |
36 |
32 |
52 |
60 |
44 |
40 |
60 |
48 |
48 |
48 |
36 |
36 |
40 |
44 |
|
68 |
52 |
40 |
40 |
52 |
52 |
44 |
36 |
48 |
48 |
36 |
40 |
48 |
36 |
44 |
40 |
44 |
|
56 |
56 |
36 |
40 |
40 |
56 |
44 |
0 |
44 |
64 |
44 |
40 |
32 |
40 |
48 |
40 |
|
|
72 |
40 |
44 |
48 |
40 |
52 |
56 |
52 |
40 |
60 |
52 |
52 |
48 |
36 |
40 |
40 |
|
|
32 |
48 |
36 |
32 |
56 |
48 |
44 |
64 |
48 |
32 |
44 |
32 |
52 |
52 |
44 |
40 |
|
|
52 |
52 |
68 |
36 |
64 |
36 |
52 |
32 |
36 |
44 |
32 |
56 |
40 |
72 |
60 |
40 |
|
|
36 |
40 |
44 |
36 |
36 |
56 |
52 |
44 |
36 |
44 |
40 |
48 |
36 |
44 |
32 |
40 |
|
|
52 |
48 |
52 |
36 |
40 |
40 |
48 |
48 |
32 |
48 |
40 |
48 |
32 |
40 |
36 |
40 |
|
|
48 |
36 |
52 |
56 |
40 |
68 |
48 |
32 |
44 |
48 |
40 |
48 |
52 |
48 |
40 |
40 |
Таблица 2
|
Балл по математике |
0-10 |
10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
60-70 |
70-80 |
|
Частота |
3 |
1 |
3 |
115 |
199 |
65 |
39 |
10 |
Процесс анализа представленных статистических данных начинается с построения самого интервального вариационного ряда по частоте по следующим принципам. Просматривая результаты наблюдений, находим, что наибольшим значением признака является х наиб. = 79, а наименьшим – х наим = 0. Найдем размах вариации R = 79 – 0 = 79. Очевидно, что балл по математике абитуриентов находится в пределах от 0 до 79. Далее находим количество частичных интервалов. Приблизительное число k интервалов можно оценить исходя из объема выборки по формуле Стержеса: k = 1 + 3,32·lg n. По нашим данным k ≈ 8.
Рассчитываем длину h частичных интервалов. Поскольку предпочтительнее ряды с интервалами одинаковой ширины, то
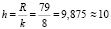 .
.
Для каждого интервала устанавливаем его верхнюю и нижнюю границы. За начало первого интервала хнач можно принять значение хнаим или хнач = хнаим – 0,5h. В нашем распределении хнач = хнаим – 5 = 0–5 = – 5 – отрицательное, поэтому возьмем хнач = хнаим = 0. Промежуточные интервалы получаем, прибавляя к концу предыдущего интервала длину частичного интервала h . Прибавив к началу первого интервала шаг, получим верхнюю границу первого интервала и одновременно нижнюю границу второго интервала. Выполняя последовательно указанные действия, находим границы последующих интервалов до тех пор, пока перекрываем хнаиб. = 79.
Просматривая результаты наблюдений, устанавливаем, сколько значений признака попало в каждый конкретный интервал. При этом попавшими в интервал считаем значения признака, большие или равные нижней границе и меньшие верхней границы.
Интервальный вариационный ряд по частоте представлен в табл. 2.
Строим гистограмму частот данного интервального ряда. Гистограммой частот представляет собой ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны плотности частоты. Для построения гистограммы строим таблицу плотности частот, при этом плотность частоты – это частота, приходящаяся на единицу величины интервала. Распределение плотностей частоты представлено в табл. 3.
Строим гистограмму частот данного вариационного ряда в прямоугольной системе координат, при этом по оси абсцисс откладываем частичные интервалы баллов абитуриентов, а по оси ординат – плотность частоты на каждом из промежутков. Гистограмма частот представлена на рис. 1.
Использование плотности частоты для построения гистограммы оправдано ее свойством, а именно: площадь данной ступенчатой фигуры равна объему выборки, т.е. в нашем распределении числу 435. Нахождение такой важной характеристики статистического распределения, как моды, помощью гистограммы, становится возможным. Модой, как правило, называют наиболее часто встречающееся значение признака в совокупности (в рассматриваемом распределении – наиболее часто встречающийся балл по математике у абитуриентов). Значение моды вариационного ряда определяется как значение признака, имеющего наибольшую частоту. Гистограмма показывает, что мода признака находится на промежутке от 40 до 50 баллов, т.е. данный промежуток является «подозрительным» на наличие моды. Примерное значение моды найдем с помощью нехитрых построений, а именно: находим прямоугольник с наибольшей частотой; соединяем отрезками вершины этого прямоугольника с соответствующими вершинами двух соседних прямоугольников; получаем точку пересечения этих отрезков (диагоналей трапеции); находим абсциссу построенной точки (рис. 1).
Мода нашего ряда примерно равна 43,75 и показывает, что наиболее часто в выборочной совокупности средний балл по математике будет примерно равен 44.
Медианой интервального вариационного ряда называют значение признака, приходящегося на середину ряда наблюдений. Графически примерное значение медианы определяется по кумуляте. Кумулята накопленных частот – это кривая накопленных частот. Для построения кумуляты частот соединяем точки 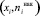 , причем кривая начинается с точки, абсцисса которой равна началу первого интервала, а ордината – накопленной частоте, равной нулю. Другие точки кривой соответствуют концам интервалов. Для построения кумуляты строим кумулятивный ряд (табл. 4).
, причем кривая начинается с точки, абсцисса которой равна началу первого интервала, а ордината – накопленной частоте, равной нулю. Другие точки кривой соответствуют концам интервалов. Для построения кумуляты строим кумулятивный ряд (табл. 4).
Кумулята данного распределения представлена на рис. 2.
Медиана может быть найдена как значение признака, для которого  . В точке на оси ординат, которая соответствует половине накопленной частоты, восстанавливаем перпендикуляр к этой оси и продолжаем его до пересечения с кумулятой. Из точки пересечения опускаем перпендикуляр на ось абсцисс; координата данной точки и будет являться медианой. Медиана исследуемого вариационного ряда, равная 45 (рис. 2), показывает, что половина выборочной совокупности имеет балл по математике, меньший 45, а другая половина – больший 45.
. В точке на оси ординат, которая соответствует половине накопленной частоты, восстанавливаем перпендикуляр к этой оси и продолжаем его до пересечения с кумулятой. Из точки пересечения опускаем перпендикуляр на ось абсцисс; координата данной точки и будет являться медианой. Медиана исследуемого вариационного ряда, равная 45 (рис. 2), показывает, что половина выборочной совокупности имеет балл по математике, меньший 45, а другая половина – больший 45.
Полезным для получения выводов о характере выборочной совокупности является вычисление средних характеристик, в частности, средней арифметической. Средней арифметической интервального вариационного ряда называют число:
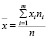 ,
,
где хi – середины интервалов, ni – соответствующие им частоты, n – объем выборки. Средняя арифметическая для нашего ряда, примерно равная 44,672, характеризует средний балл по математике у абитуриентов и может быть использована для нахождения других числовых характеристик, таких как дисперсия, коэффициент вариации и т.д.
Проведенное нами статистическое исследование признака «балл по математике» абитуриентов ФБГОУ ШГПИ в 2014 году показало важность и принципиально высокое значение статистических методов для получения научных и практических выводов, позволяющих более целесообразно и качественно организовать преподавание математических дисциплин на факультете. Возникает возможность проводить сравнительный анализ признака по годам для поступающих в институт, находить другие числовые характеристики исследуемого вариационного ряда для более глубокого и тщательного изучения этого важного признака.
Таблица 3
|
Балл по математике |
0-10 |
10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
60-70 |
70-80 |
|
Плотность частоты |
0,3 |
0,1 |
0,3 |
11,5 |
19,9 |
6,5 |
3,9 |
1,0 |
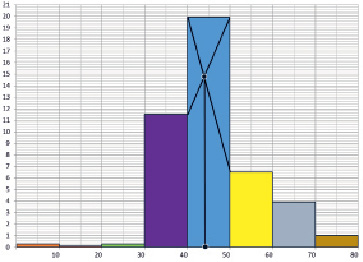
Рис. 1
Таблица 4
|
Балл по математике |
0-10 |
10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
60-70 |
70-80 |
|
Накопленная частота |
3 |
4 |
7 |
222 |
321 |
386 |
425 |
435 |
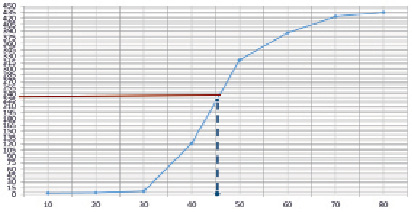
Рис. 2
Библиографическая ссылка
Бобровская А.В., Парамонов Е.В. МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ В ОБРАБОТКЕ РЕЗУЛЬТАТОВ ИТОГОВОЙ АТТЕСТАЦИИ ПО МАТЕМАТИКЕ В ШКОЛЕ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 2-4. – С. 547-550;URL: https://applied-research.ru/ru/article/view?id=8635 (дата обращения: 24.04.2024).

