Рассмотрим отдельную академическую группу студентов, которую разделим на три подгруппы по успеваемости: отлично, хорошо и удовлетворительно. Ясно, что подгруппы влияют друг на друга, наблюдается прирост одной группы за счет другой, причем прирост и уменьшение могут быть оценены численно.
Математический подход опирается на изучение решений дифференциальных и интегро-дифференциальных уравнений В. Вольтерра [1], которые нужно исследовать количественно и качественно.
Обучаясь какому-то предмету, студенты одной подгруппы влияют на успеваемость другой подгруппы, оказывая помощь друг другу в изучении учебного материала. Этот процесс можно условно назвать «борьбой за существование».
Количественный характер этого явления проявляется в заданной сфере в виде изменений численности студентов, составляющих разные подгруппы. При одних условиях эти изменения состоят из флуктуаций вокруг средних значений, при других условиях сводятся к исчезновению или прогрессирующему увеличению других подгрупп. В статье производится теоретическое изменение численности студентов в подгруппах; из этого математическими средствами выводятся возможные следствия.
Исследования относятся к целочисленным переменным, но мы будем пользоваться не дискретной математикой и теорией вероятности, исчислением бескнечно малых, математическим анализом и теорией дифференциальных уравнений.
Для того, чтобы охарактеризовать некоторую подгруппу, сделаем допущение, что студенты каждой подгруппы однородны по успеваемости. Будем также считать, что тип студента меняется со временем непрерывно. Тогда вместо разрывных целочисленных функций, представляющих численность студентов в подгруппе, можно описать непрерывной дифференци
руемой функцией. В каждый момент времени функция будет иметь ту же целую часть, что и разрывная функция.
Рассмотрим одну из подгрупп студенческой группы, которая обучается изолированно или обучается с другими подгруппами , не оказывая на них никакого влияния. Обозначим через N количество студентов, обладающих определенными знаниями и принадлежащих -ой подгруппе. Увеличение числа студентов за некоторый малый интервал времени будет пропорционально этому количеству Ni . Принимая это свойство функции и рассматривая ее как непрерывную, получаем
где εi. - постоянный коэффициент пропорциональности, отражающий скорость изменения знаний внутри подгруппы, выраженный в изменении числа студентов в подгруппе dNi/dt к общему числу студентов Ni . Назовем его коэффициентом прироста знаний в данной подгруппе. Из уравнения
получаем решение
Это решение определяет экспоненциальный закон развития обучения, состоящий в том, что если время возрастает в арифметической прогрессии, то количество знаний возрастает в геометрической прогрессии. Если εi > 0, происходит развитие студентов; если εi < 0 - студенты регрессируют и при εi = 0 наблюдается застой в образовании данной подгруппы. Коэффициент εi легко найти из уравнения (3). Если обозначить период обучения за один семестр T, то
Прологарифмируем это выражение и выразим εi
Выражение lnNi - N0i. = ΔNi назовем логафмическим приростом знаний.
Если теперь предположить, что внешняя среда меняется медленно, то для короткого промежутка времени можно считать
Кроме того, на коэффициент εi влияет количество знаний других подгрупп и мы получаем дифференциальные уравнения вида:
Будем предполагать, что коэффициент прироста знаний зависит не только от Ni , но и от значений в предшествующий период, а именно знаний , полученных в школе и Вузе до рассматриваемого момента. В результате получится система интегро-дифференциальных уравнений Вольтера.
Рассмотрим три подгруппы студентов, изучающих один предмет в пределах одной группы. Коэффициенты прироста знаний обозначим ε1, ε2, ε3. Если учебный материал, который нужно изучить в течении семестра обозначить функцией F (N1, N2, N3) и взять его равным нулю в начальный момент времени, то в качестве прироста знаний можно взять выражения ε1 - F (N1, N2, N3) γ1 - положительные постоянные, соответствующие потребности знаний в каждой из подгрупп. Получаем систему дифференциальных уравнений, описывающую развитие обучения студентов в группе:
Встает математическая задача исследования решений N1, N2, N3 этой системы при начальных знаниях и начальном распределении студентов по подгруппам N01, N02, N03.
Можно показать, что для всякого конечного интервала времени (t0, T) существует единственное решение из двух непрерывных функций, заключенных между двумя положительными числами, из которых большее не зависит от конца интервала T, т. е. N1, N2, N3 остаются ограниченными.
С одной стороны, предположим, что в интервале (t0, T) существуют три непрерывные функции N1, N2, N3 , удовлетворяющие начальным данным. Пусть N1´, N2´, N3´- числа Б, превосходящие эти начальные данные и достаточно большие для того, чтобы выполнялись неравенства:
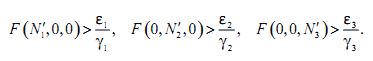
Покажем, что N1, N2, N3, не превосходят N´1, N´2, N´3. Действительно, если N1 превышает N´1, то в некоторый момент времени θ функция N достигает значения N´, и тогда 
откуда dN1/dt< 0, т. е. N1 переходит через N´1, убывая, и значит, N1 принимает значение большее, чем N´1 до момента θ, и т. к. N°1 < N´1, то N1 должна принять значение N´1 ( в силу непрерывности) до момента θ, что противоречит гипотезе, принятой относительно θ.
Следовательно, N1, N2, N3 остаются меньшими, чем числа N´1, N´2, N´3, которые не зависят от конца T интервала (t0, T).
Для удобства дальнейших рассуждений перепишем систему (7) в виде
После интегрирования получим
Поскольку Ni ограничены числами Nt , то выражения в квадратных скобках ограничены по абсолютной величине некоторым значением A, не зависящим от t, поэтому в интервале (t0, T) получим
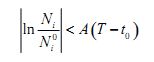
и, следовательно, 
.
Рассмотрим, что произойдет при неограниченном увеличении времани. Исключая из системы (7´) функцию F (N1, N2, N3), получим эквивалентную систему
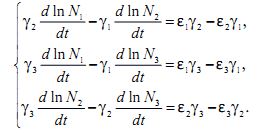
Решение этой системы можно записать так:
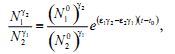
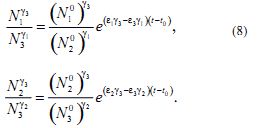
Пренебрежем случаем, когда εiγk - εkγi = 0, то есть когда скорости усвоения знаний пропорциональны скоростям усвоения знаний во всех трех группах замкнутой системы, что маловероятно и предположим, что
Тогда, согласно формуле (8), имеем
Известно, что N1 ограничено, поэтому N2 и N3 стремятся к нулю.
Итак, подгрупп, у которой - имеет меньшее значение со временем исчезает, ее студенты переходят в группу с более высокой успеваемостью. Чтобы подгруппа продолжала существовать, нужно, чтобы у нее сохранялся высокий коэффициент ε/γ
Cписок литературы
- В. Вольтерра. Математическая теория борьбы за существование. М.: Изд-во «Наука». 1976. 286 с.
Библиографическая ссылка
Добрынина Н.Ф. СИНЕРГЕТИКА В ВЫСШЕМ ОБРАЗОВАНИИ // Международный журнал прикладных и фундаментальных исследований. – 2010. – № 12. – С. 63-65;URL: https://applied-research.ru/ru/article/view?id=991 (дата обращения: 03.12.2024).