Современные параллельные вычислительные системы, функционирующие в модулярных кодах, позволяют достичь максимальной производительности за счет обработки малоразрядных остатков. Стремление обеспечить предельные скоростные характеристики приводит к усложнению устройства, что негативно влияет на надежность его функционирования. Повысить отказоустойчивость параллельных вычислительных систем можно за счет применения избыточных модулярных кодов, в том числе кодов полиномиальной системы классов вычетов (ПСКВ).
Цель исследования
Коды полиномиальной системы классов вычетов за счет введения избыточных оснований позволяют обнаруживать и корректировать ошибки, возникающие в процессе вычислений из-за отказов оборудования. Однако для устранения последствий потока отказов такая избыточность становится достаточно большой. Решить эту проблему можно за счет проведения реконфигурации, то есть перераспределения вычислительной нагрузки между работоспособными каналами. Однако, отсутствие эффективного алгоритма пересчета значений ортогональных базисов (ОБ) не позволяют широко использовать реконфигурацию непозиционных вычислительных систем. Поэтому разработка алгоритма пересчета ОБ при проведении управляемой деградации непозиционной вычислительной системы является актуальной задачей.
Материалы и методы исследования
Код полиномиальной системы классов вычетов относится к непозиционным кодам. Кодовая комбинация ПСКВ представляется в виде набора остатков полиномам A(z) по основаниям, в качестве которых выбраны неприводимые полиномы pi(z). Тогда
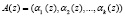 , (1)
, (1)
где 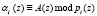 ; i = 1, 2, …, n.
; i = 1, 2, …, n.
Произведение оснований кода ПСКВ позволяет определить рабочий диапазон
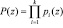 . (2)
. (2)
Проведенный анализ работ [1, 3, 6] показал, что коды ПСКВ наиболее эффективно реализуют такие модульные операции как сложение, вычитание и умножение по модулю. В этом случае для кода ПСКВ справедливо
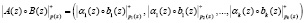 , (3)
, (3)
где 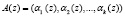 ;
;
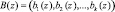 ;
;
 – модульная операция.
– модульная операция.
Для обеспечения отказоустойчивости в код ПСКВ вводят избыточные основания, удовлетворяющие условию
 . (4)
. (4)
В результате происходит расширение рабочего диапазона до полного диапазона
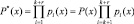 . (5)
. (5)
Так как ошибка переводит правильный 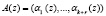 в ошибочный полином
в ошибочный полином 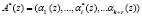 , лежащий вне рабочего диапазона, то, зная местоположение искаженного полинома А*(z), можно однозначно определить модуль pi(z), по которому произошла ошибка, а также ее глубину.
, лежащий вне рабочего диапазона, то, зная местоположение искаженного полинома А*(z), можно однозначно определить модуль pi(z), по которому произошла ошибка, а также ее глубину.
Применение корректирующих кодов ПСКВ наиболее эффективно при исправлении однократных ошибок. Однако при возникновении потока отказов такой подход не может обеспечить высокую отказоустойчивость. Решением данной проблемы является использование разработанный метод реконфигурации, который позволяет сохранять работоспособное состояние при возникновении отказов за счет снижения в допустимых пределах основных показателей качества функционирования. Данный метод перераспределения вычислительной нагрузки содержит следующие этапы [4, 5]: – обнаружение ошибочного вычислительного канала ПСКВ; – отключение отказавшего канала; – перераспределение вычислительной нагрузки между оставшимися модулями ПСКВ; – для организации обратного преобразования из кода ПСКВ в позиционный код пересчитать ортогональные базисы для деградируемой системы.
Если первые три этапа управляемой деградации структуры ВС можно достаточно легко реализовать в ПСКВ, то последний этап – во многом будет определять эффективность противодействия потоку отказов. В настоящее время известно несколько алгоритмов, позволяющих осуществлять перерасчет значений ортогональных базисов при изменении количества информационных и контрольных оснований ПСКВ [5].
В работе [3] представлено устройство для вычисления сумм парных произведений, функционирующее в ПСКВ. В основу работы данного устройства положено свойство сравнимости ортогональных базисов избыточной и безизбыточной систем ПСКВ.
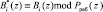 , (6)
, (6)
где Bi(z) – ортогональный базис избыточной системы ПСКВ; 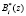 – ортогональный базис безизбыточной ПСКВ.
– ортогональный базис безизбыточной ПСКВ.
Такой подход позволяет перейти к вычислению в системе ПСКВ с меньшим числом модулей. Это свойство было положено в алгоритм пересчета ортогональных базисов модулярного кода при расширении системы оснований, который приведен в работе [1]. При расширении системы оснований необходимо осуществить пересчет ортогональных базисов 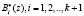 , при заданных начальных значениях
, при заданных начальных значениях 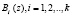 системы оснований
системы оснований 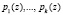 . Используя свойство сравнимости ортогональных базисов, имеем
. Используя свойство сравнимости ортогональных базисов, имеем
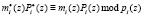 (7)
(7)
где mi(z) и 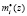 – вес ортогонального базиса в безизбыточной и расширенной ПСКВ.
– вес ортогонального базиса в безизбыточной и расширенной ПСКВ.
Так как значения 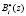 расширенной системы оснований и
расширенной системы оснований и 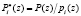 являются взаимно простыми с основанием pi(z), то выражение (7) можно переписать в виде
являются взаимно простыми с основанием pi(z), то выражение (7) можно переписать в виде
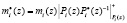 (8)
(8)
С учетом того, что 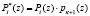 , получаем
, получаем
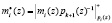 (9)
(9)
Тогда, пересчитанная величина ортогонального базиса равна
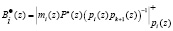 (10)
(10)
Так как в (10) используются константы, то для реализации пересчета была предложена двухслойная нейронная сеть, которая показана на рис. 1.
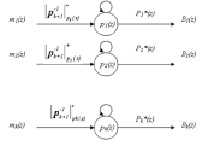
Рис. 1. Нейронная сеть для пересчета ортогональных базисов ПСКВ
В работе [1] задача пересчета сводится к преобразованию ортогональных базисов Bi(z), где i = 1, …, k, из пространства
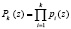 ,
,
в ортогональные базисы 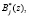 где i = 1, …, k –1, определяемые диапазоном
где i = 1, …, k –1, определяемые диапазоном
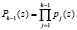 .
.
Уменьшение диапазона Pk(z), определяемое оставшимися рабочими основаниями pj(z) приводит к изменению значений «деградируемых» ортогональных базисов известно, что
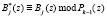 . (11)
. (11)
Проведенные исследования показали, что формирование новых ортогональных базисов можно осуществить с помощью многотактовых кодовых фильтров (МКФ). Такие фильтры содержат элементы трех видов: сумматоры по модулю два на два входа и один выход, устройство задержки символов на один временной такт, устройства умножения символов на величину 0, либо 1. Пусть полиномиальная форма делителя имеет вид:
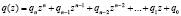 , (12)
, (12)
где коэффициенты qi для i = 1, …, n лежат в поле GF(p).
Тогда все операции сложения должны быть выполнены в поле GF(p), и каждая ячейка регистра сдвига должна содержать элемент из GF(p). Далее, результат на выходе сумматора, формирующего член обратной связи, нужно умножить на 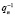 . Наконец для каждого нулевого qi, i > n, член обратной связи должен быть умножен на – qi. Сумма полученного произведения с результатом выхода предыдущей ячейки является входным значением i-й ячейки регистра, где i меняется от 0 до n – 1. Схема МКФ показана на рис. 2.
. Наконец для каждого нулевого qi, i > n, член обратной связи должен быть умножен на – qi. Сумма полученного произведения с результатом выхода предыдущей ячейки является входным значением i-й ячейки регистра, где i меняется от 0 до n – 1. Схема МКФ показана на рис. 2.
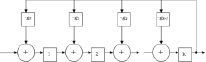
Рис. 2. Обобщенная схема МКФ
Однако данный метод вычисления обладает недостатком – для пересчета ОБ необходимо постоянно изменять структуру вычислительного устройства, постоянно подавая на его вход ортогональные вектора Bi(z), i = 1, …, k исходной ПСКВ. Отсюда следует актуальность разработки нового алгоритма пересчета ОБ, позволяющего осуществлять управляемую деградацию ВС ПСКВ.
В разработанном алгоритме пересчета ОБ применяется свойство ортогональности, а также алгоритм вычисления ОБ. Согласно последнему для вычисления ОБ необходимо знать
 . (13)
. (13)
Для выполнения условия ортогональности используют вес ОБ mi(z), такого, что
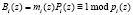 . (14)
. (14)
Исходя из последнего условия, выражение (14) можно представить как
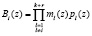 , (15)
, (15)
где ml(z) – вес l-го основания ПСКВ, определяемый соотношением
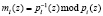 . (16)
. (16)
Очевидно, что для выполнения условия (14) необходимо соблюдение равенства
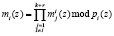 . (17)
. (17)
Следовательно, для пересчета ортогональных базисов при построении деградируемого СП ПСКВ необходимо использовать значения 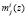 , то есть обратных величин оснований pl(z) по модулю pi(z).
, то есть обратных величин оснований pl(z) по модулю pi(z).
Результаты исследования и их обсуждение
Пусть задан код с модулями 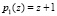 ,
, 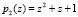 ,
, 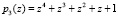 ,
, 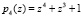 ,
, 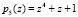 . и все основания СП ПСКВ находятся в исправном состоянии. Рассмотрим реализацию алгоритма вычисления веса ортогонального базиса B5(z). Для вычисления данного ортогонального базиса была получена константы
. и все основания СП ПСКВ находятся в исправном состоянии. Рассмотрим реализацию алгоритма вычисления веса ортогонального базиса B5(z). Для вычисления данного ортогонального базиса была получена константы
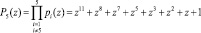 .
.
Тогда остаток 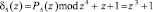 , а индексное представление будет равно
, а индексное представление будет равно 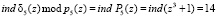 . Для выполнения условие (14) определим значение индекса веса ортогонального базиса m5(z) такое, чтобы
. Для выполнения условие (14) определим значение индекса веса ортогонального базиса m5(z) такое, чтобы
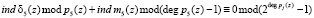 .
.
В этом случае индекс веса ортогонального базиса будет определяться из условия
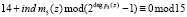 .
.
Таким образом, ind m5(z) = 1. Это означает, что величина веса ортогонального базиса B5(z) равна m5(z) = z. Тогда ортогональный базис составит
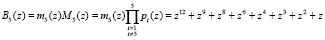 .
.
Для вычисления B5(z) были использованы константы и их индексное представление:
– 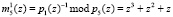 ;
;
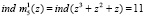 .
.
– 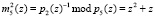 ;
;
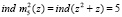 .
.
– 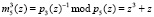 ;
;
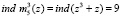 .
.
– 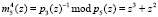 ;
;
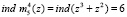 .
.
Проведем расчет веса ортогонального базиса, используя разработанный алгоритм
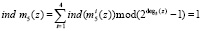 .
.
Таким образом, вес ортогонального базиса B5(z) равен 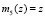 .
.
Аналогичным образом можно произвести вычисление веса ортогонального базиса при постепенной управляемой деградации структуры СП ПСКВ при потоке отказов. Очевидно, чтобы использование разработанного алгоритма индексного представления веса ОБ позволяет повысить скорость выполнения данной немоудльной операции.
Определим схемные затраты, которые будут затрачены на реализацию алгоритма пересчета ОБ, приведенные в работе [2]. В состав этого блока пересчета входят два блока памяти, (n –2) умножителя по модулю pi(z), а также один позиционный умножитель. Тогда схемные затраты на блок расчета ортогонального базиса определяются
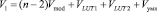 , (18)
, (18)
где Vmod – схемные затраты на умножители по модулю pi(z); VLUT – схемные затраты на блок памяти LUT; Vумн – схемные затраты на позиционный сумматор.
Значит для рассмотренного кода ПСКВ данных схемные затраты на блок вычисления ОБ, использующего мультипликативный алгоритм потребуется V1 = 810 элементов.
Схемные затраты необходимые на построение блока вычисления ОБ, использующий разработанный алгоритм пересчета веса, будут определяться
 , (19)
, (19)
где VSUmod – схемные затраты на сумматор по модулю 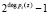 ; Vрег – схемные затраты на регистр;Vпроеб – схемные затраты на преобразователь «индекс-элемент».
; Vрег – схемные затраты на регистр;Vпроеб – схемные затраты на преобразователь «индекс-элемент».
Проведенные исследования показали, что схемные затраты на реализацию разработанного алгоритма V2 = 681 элемент. Очевидно, что выигрыш в схемных затратах разработанного алгоритма вычисления веса ОБ составит К = V1/V2 = 1,19.
Заключение
В работе проведен анализ основных методов пересчета ортогональных базисов при постепенной деградации СП ПСКВ из-за потока отказов. Показано, что известные ранее алгоритмы имеют значительные схемные затраты. С целью решения данной проблемы был разработан алгоритм пересчета весов ОБ, на основе использования индексного представления. Проведенные исследования показали, что при использовании разработанного алгоритма пересчета веса ОБ, схемные затраты будут сокращены в 1,19 раза по сравнению с алгоритмом, использующем линейку умножителей по модулю.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-37-50032.
Библиографическая ссылка
Белов С.П., Саркисов А.Б., Хахалев Т.А., Калмыков И.А., Ряднов С.А. РАЗРАБОТКА АЛГОРИТМА ПЕРЕСЧЕТА ОРТОГОНАЛЬНЫХ БАЗИСОВ ПРИ ПРОВЕДЕНИИ УПРАВЛЯЕМОЙ ДЕГРАДАЦИИ НЕПОЗИЦИОННОЙ ВЫЧИСЛИТЕЛЬНОЙ СИСТЕМЫ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 11-2. – С. 193-197;URL: https://applied-research.ru/ru/article/view?id=10463 (дата обращения: 26.04.2024).

