Для обеспечения эффективной работы объектов добычи и транспортировки углеводородов, расположенных за Полярным Кругом, используются комплексы мониторинга, контроля и управления удаленными экологически опасными объектами. При этом для обеспечения связи с такими объектами используют низкоорбитальные системы спутниковой связи (ССС). Чтобы предотвратить возможность перехвата, задержки и навязывания управляющих команд спутником-нарушителем, в работах [1, 2] предлагается использовать систему опознавания «свой-чужой».
Чтобы повысить отказоустойчивость системы опознавания «свой-чужой» предлагается использовать модулярные корректирующие коды. Так как модулярные коды при выполнении вычислений в качестве операндов используют остатки, то разрабатываемая программно-аппаратная система определения статуса космического аппарата (КА) должна обеспечивать преобразование из позиционного кода в модулярный код. Поэтому разработка моделей прямого преобразователя из позиционного кода в модулярный код для отказоустойчивой системы аутентификации спутника является актуальной задачей.
Цель исследования
Очевидно, что использование системы опознавания «свой-чужой» на платформе КА приводит к увеличению схемных затрат. Чтобы обеспечить устойчивость к отказам, в условиях жестких масса-габаритных показателей, предлагается использовать избыточные модулярные коды. Такие коды, на основе параллельной и независимой обработки остатков в вычислительных каналах, способны обнаруживать и корректировать ошибки, которые возникают в процессе вычислений.
Чтобы повысить эффективность работы системы опознавания «свой-чужой», необходимо провести изучение основных методы и алгоритмов, предназначенных для преобразования позиционного кода в модулярный код.
Поэтому целью данной работы является разработка моделей прямого преобразователя из позиционного кода в модулярный код для отказоустойчивой системы аутентификации спутника, применение которых позволит обосновать выбор алгоритма, обладающего минимальными схемными временными затратами.
Материалы и методы исследования
Для предотвращения последствий сбоев и отказов, которые могут возникнуть в процессе работы системы опознавания «свой-чужой», в работах [1, 2] предлагается использовать коды классов вычетов. Характерной чертой таких кодов является то, что вычисления производятся параллельно и по независимым вычислительным каналам. Таким образом, модулярные коды осуществляют параллельную обработку остатков. Значит, выбор эффективного алгоритма выполнения процедуры получения остатков из позиционного кода позволит повысить эффективность всей запросно-ответной системы.
Модулярные коды системы остаточных классов (СОК) представляют собой совокупность останков, которые были получены при делении операнда А на основания системы р1, р2, ..., рk [3, 5]. Тогда справедливо равенство
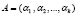 , (1)
, (1)
где 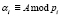 ;
; 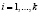 ; НОД(рi, pj) = 1, i ≠ j.
; НОД(рi, pj) = 1, i ≠ j.
Основным достоинством кодов СОК является ускоренное выполнение модульных операций. Пусть даны два числа 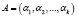 и
и 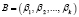 , представленные в коде СОК. Тогда справедливо
, представленные в коде СОК. Тогда справедливо
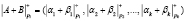 , (2)
, (2)
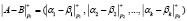 , (3)
, (3)
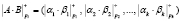 , (4)
, (4)
где 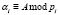 ;
; 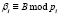 .
.
Для реализации вычислительного процесса с использованием СОК необходимо осуществить преобразование из позиционной системы счисления (ПСС) в модулярный и обратно. Согласно [5, 8, 9] такие операции являются немодульными и относятся к классу позиционных операций, которые являются наиболее трудоемкими в непозиционной системе классов вычетов. Одним из самых простых методов получения остатка является метод последовательного деления. Образование остатка 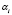 осуществляется следующим образом:
осуществляется следующим образом:
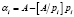 , (5)
, (5)
где 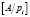 – наименьшее целое от деления А на основание СОК pi;
– наименьшее целое от деления А на основание СОК pi; 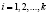 .
.
Наряду с последовательным методом получения остатка можно выделить и параллельные методы. Все множество методов перевода из позиционной системы счисления в систему классов вычетов можно свести к нескольким основным группам. Как показано в работах [3, 8, 9], основу первой группы методов перевода составляет метод понижения разрядности операнда. теорема, согласно которой вычисление остатка осуществляется с помощью итерационного алгоритма. Для этого необходимо определить остатки от деления на pj степеней основания, которые дадут набор чисел Ci, 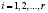 . Если остаток от деления степени основания Ci превосходит половину модуля pj, то в качестве значения Ci необходимо взять число, дополняющее до значения pj, со знаком минус. Значения Ci можно знать заранее, и они являются константами для выбранной системы счисления. Количество разрядов Ci определяется разрядностью исходного числа А. Затем цифры исходного числа умножаются на соответствующие числа Ci, полученная сумма определяется
. Если остаток от деления степени основания Ci превосходит половину модуля pj, то в качестве значения Ci необходимо взять число, дополняющее до значения pj, со знаком минус. Значения Ci можно знать заранее, и они являются константами для выбранной системы счисления. Количество разрядов Ci определяется разрядностью исходного числа А. Затем цифры исходного числа умножаются на соответствующие числа Ci, полученная сумма определяется
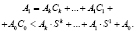 (6)
(6)
Таким образом, для получения 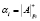 предлагается использовать модель
предлагается использовать модель
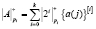 ,
, 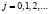 (7)
(7)
Основу второй группы составляют методы, обеспечивающие пространственное распределение вычислительного процесса перевода из ПСС в модулярный код. Отказ от обратных связей позволяет повысить скорость выполнения операции перевода. В работе [7] предложена математическая модель вычислительного устройства, реализующего прямое преобразование позиционного двоичного кода в код СОК. Число слоев в такой сети определяется количеством итераций m, необходимых для преобразования входных данных. В этом случае итеративный алгоритм преобразования A по модулю p определяется выражением
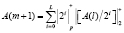 , (8)
, (8)
где 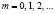 – число итераций; L = log2 A(m).
– число итераций; L = log2 A(m).
Однако, обеспечивая пространственное распределение вычислительного процесса перевода из ПСС в модулярный код, данные методы требуют значительных аппаратурных затрат, что может негативно сказаться на надежности работы непозиционного процессора в целом. Для оценки эффективности рассмотренных последовательного и параллельного методов получения остатка разработаем модели.
Результаты исследования и их обсуждение
Для создания и проектирования цифровых устройств широко применяются программируемые логические интегральные схемы (ПЛИС) [4]. Это связано с тем, что логика работы ПЛИС не определяется при ее изготовлении, а создается в процессе проектирования на языках описания аппаратуры (Verilog HDH, VHDL, AHDL и др.).
Для задачи выбора метода порогового разделения данных при проектировании цифровых схем выбраны следующие критерии оценки: время разделения данных при реализации на ПЛИС; количество затраченных логических элементов(LEs) ПЛИС; потребляемая мощность ПЛИС Вт. Данные критерии помогут оценить требуемые ресурсы ПЛИС. В ходе эксперимента описание аппаратуры проводилось на языке Verilog HDL. Для моделирования выбран процессор фирмы Altera из семейства Cyclone III модели EP3C80F484C6 [6]. Следующим шагом для моделирования является разработка программы для их реализации на языке описания аппаратуры Verilog HDL. Рассмотрим каждую модель прямого преобразователя из ПСС в модулярный код.
На рис. 1 представлена модель функционального устройства вычисления остатка от деления последовательным методом. Так как вычисление значения аккумулятора происходит с положительной обратной связью, то необходима синхронизация, поэтому расчет для каждого разряда входной шины данных происходит по положительному фронту внешнего генератора частоты тактового сигнала (рис. 2).
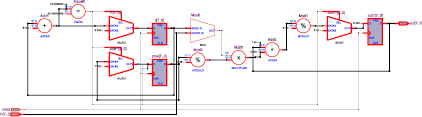
Рис. 1. Модель функционального устройства вычисления остатка от деления последовательным методом
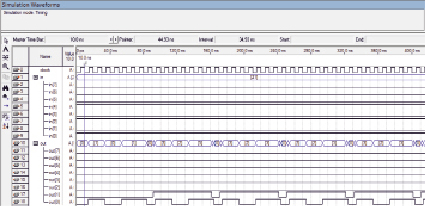
Рис. 2. Временная диаграмма функционального устройства вычисления остатка от деления последовательным методом
Из временной диаграммы видно, что для вычисления остатка от деления потребуется n тактов генератора, и вычисления в каждом из тактов происходят примерно за 8.893 нс. По остальным критериям оценки функциональных устройств получены следующие результаты: занято 113 Les; потребляемая мощность 0,116952157113843 Вт.
Для увеличения скорости нахождения остатков вычисления производятся в несколько потоков. На рис. 3 представлена модель функционального устройства вычисления остатков от деления с применением двух потоков, реализующая метод (7).
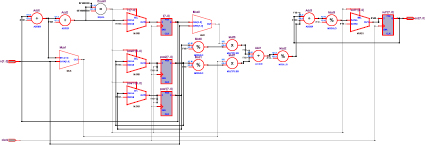
Рис. 3. Модель функционального устройства вычисления остатков с применением двух потоков
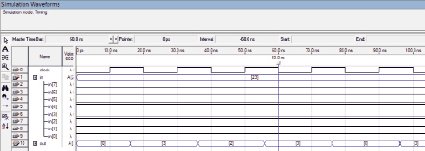
Рис. 4. Временная диаграмма функционального устройства вычисления остатка от деления с применением двух потоков
На рис. 4 представлена временная диаграмма разработанной модели функционального устройства вычисления остатка от деления с применением двух потоков. Из временной диаграммы видно, что для вычисления требуется в два раза меньше импульсов генератора тактовой частоты. Вычисления при каждом импульсе происходят примерно за 6 нс. По остальным критериям оценки функциональных устройств получены следующие результаты: занято 165 Les; потребляемая мощность 0.116952157113843 Вт.
При использовании метода понижения разрядности и разделении процесса вычисления остатка на n потоков нет необходимости подключать внешний генератор для вычисления каждого бита входной шины. На рис. 5 представлена модель функционального устройства вычисления остатков от деления с применением n потоков.
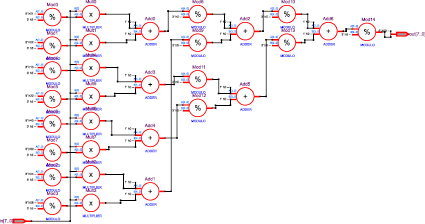
Рис. 5. Модель функционального устройства вычисления остатков от деления с применением n потоков
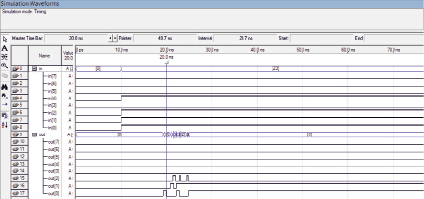
Рис. 6. Временная диаграмма функционального устройства вычисления остатка от деления с применением двух потоков
На рис. 6 представлена временная диаграмма разработанной модели функционального устройства вычисления остатка от деления с применением n потоков. Из временной диаграммы видно, что для вычисления требуется 15 нс. По остальным критериям оценки функциональных устройств получены следующие результаты: занято 82 Les; потребляемая мощность 0,116858249665486 Вт.
Из рассмотренных моделей функциональных устройств прямого преобразования из ПСС в СОК можно сделать вывод, что для вычисления остатков от целочисленного деления на произвольный набор модулей предпочтительно использовать параллельный метод нахождения остатков с применением дерева сумматоров.
Заключение
В статье рассмотрены вопросы разработки моделей прямого преобразователя из позиционного кода в модулярный код для отказоустойчивой системы аутентификации спутника. Данные преобразователи являются необходимой частью отказоустойчивой системы опознавания «свой-чужой», функционирующей в модулярном коде. Проведенные исследования разработанных моделей показали, что применение параллельных методов вычисления остатков позволяет сократить в 1,3–2 раза число используемых LEs; а также в 1,000803 потребляемую мощность, что окажет положительное влияние на надежность работы запросно-ответной системы.
Библиографическая ссылка
Калмыков М.И., Кочеров Ю.Н., Малышев Б.Ю., Кухтин О.К., Алиев Г.С., Калмыков И.А., Ефимович А.В. РАЗРАБОТКА МОДЕЛЕЙ ПРЯМОГО ПРЕОБРАЗОВАТЕЛЯ ИЗ ПОЗИЦИОННОГО КОДА В МОДУЛЯРНЫЙ КОД ДЛЯ ОТКАЗОУСТОЙЧИВОЙ СИСТЕМЫ АУТЕНТИФИКАЦИИ СПУТНИКА // Международный журнал прикладных и фундаментальных исследований. – 2017. – № 7-1. – С. 22-27;URL: https://applied-research.ru/ru/article/view?id=11684 (дата обращения: 24.04.2024).

