Известно, что поверхности туннеля являются сложными криволинейными поверхностями, которые должны соответствовать наперед заданным требованиям. Конструирование туннельных поверхностей подземных сооружений осуществляется закрытым и горным способами [1]. Туннельные поверхности при закрытом способе сооружают одновременно на нескольких участках, это дает возможность сокращения сроков строительства [2]. На всех участках с поверхности над осью туннеля закладывают ствол шахты и штольней соединяют его со строящимся туннелем. При горном способе поверхность туннелей разрабатывают буровзрывным методом или механизированным инструментом, после этого немедленно выполняют временное крепление и контура выработки, а затем возводят обделку туннеля [3]. Данные способы требуют разработки конструкции поверхности туннелей. Вследствие чего конструирование поверхности туннеля представляет собой сложную криволинейную поверхность, которая должна отвечать заданным требованиям, а конструкция поверхности туннеля требует значительных затрат времени [4]. В работе предлагается новый способ построения поверхности туннеля в соответствии с предопределенными условиями с использованием биквадратичного преобразования плоскости, что позволяет описать конструкцию каждой секции туннеля одним уравнением [5]. Конструирование и строительство поверхности туннеля требует значительного времени и затрат, поэтому совершенствование методов конструирования поверхностей подземных сооружений является актуальной задачей в шахтостроении [6].
Цель исследования: в результате исследований получить новый метод конструирования поверхности туннеля по наперед заданным условиям с использованием биквадратичного преобразования плоскости, который позволит описать конструирование каждого сечения туннеля одним уравнением.
Материалы и методы исследования
Квадратичные преобразования плоскости исследованы достаточно и нашли применение в прикладной геометрии, а также в науке и технике. Однако исследованию и применению четыре – четырехзначных соответствий и биквадратичных преобразований плоскости исследованы мало.
Сущность предлагаемого метода моделирования биквадратичных преобразований плоскости, порождаемых бинарным отображением двух поверхностей второго порядка, заключается в следующем.
В евклидовом трехмерном пространстве E3 задаются две поверхности второго порядка 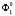 и
и 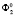 , уравнения которых имеют вид
, уравнения которых имеют вид
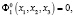 (1)
(1)
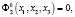 (2)
(2)
где x1, x2, x3 – декартовые координаты;
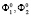 – непрерывные многочлены второго порядка.
– непрерывные многочлены второго порядка.
На плоскости П1 отметим точку А и через эту точку проведём вертикальный луч s, который пересекает заданные поверхности 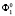 и
и 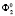 соответственно в точках
соответственно в точках 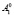 и
и 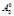 ,
, 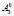 и
и 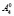 . Поверхность второго порядка
. Поверхность второго порядка 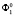 вращаем вокруг оси ординаты так, чтобы положительное направление оси аппликаты совпадало с положительным направлением оси абсциссы.
вращаем вокруг оси ординаты так, чтобы положительное направление оси аппликаты совпадало с положительным направлением оси абсциссы.
Другими словами, поверхность второго порядка 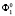 подвергается пространственному преобразованию γ1 (вращению вокруг оси ординаты под углом 900), матрица которого задается уравнением
подвергается пространственному преобразованию γ1 (вращению вокруг оси ординаты под углом 900), матрица которого задается уравнением
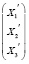 =
= 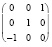
 . (3)
. (3)
Получим новое положение поверхности второго порядка 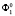 и точки
и точки 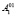 ,
, 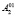 , которые соответствуют точкам
, которые соответствуют точкам 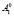 и
и 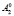 . Точки
. Точки 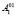 и
и 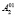 проецируем вертикальными лучами на плоскость П1, получим точки A1 и A2. Вращаем вокруг оси абсциссы вторую поверхность второго порядка
проецируем вертикальными лучами на плоскость П1, получим точки A1 и A2. Вращаем вокруг оси абсциссы вторую поверхность второго порядка 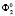 так, чтобы положительное направление оси аппликаты совпадало с положительным направлением оси ординаты.
так, чтобы положительное направление оси аппликаты совпадало с положительным направлением оси ординаты.
Таким образом, поверхность 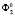 подвергаем пространственному преобразованию γ2, заданному матричным уравнением
подвергаем пространственному преобразованию γ2, заданному матричным уравнением
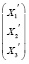 =
= 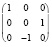
 . (4)
. (4)
После преобразования получим новое положение поверхности второго порядка 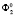 и точки
и точки 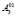 ,
, 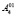 , которые соответствуют точкам,
, которые соответствуют точкам, 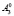 и
и 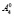 . Проецируем точки
. Проецируем точки 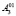 и
и 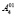 вертикальными лучами на плоскость П1, получим точки A3 и A4.
вертикальными лучами на плоскость П1, получим точки A3 и A4.
Через точки A1, A2 и A3, A4 проводим прямые, параллельные соответственно осям координат ОХ2, ОХ1. Получим четырехугольник с вершинами 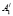 ,
, 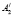 и
и 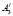 ,
, 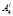 .
.
В результате последовательного выполнения вышеизложенного конструктивного аппарата, каждая точка A плоскости П1 преобразуется в четыре точки 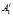 ,
, 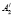 и
и 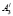 ,
, 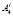 плоскости
плоскости 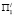 .
.
Учитывая двухпараметрическое множество точек совмещенной плоскости 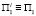 , получим биквадратичное преобразование плоскости, обозначенное буквой L. Аналогичным образом можно показать, что в обратном направлении каждая точка A/ плоскости
, получим биквадратичное преобразование плоскости, обозначенное буквой L. Аналогичным образом можно показать, что в обратном направлении каждая точка A/ плоскости 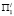 преобразуется в четыре точки плоскости П1. Это преобразование обозначим буквой L/.
преобразуется в четыре точки плоскости П1. Это преобразование обозначим буквой L/.
С использованием предложенной выше пространственной конструктивной схемы нами получены различные виды канонических биквадратичных преобразований L, L/ плоскости.
Разработанная пространственная конструктивная схема отображения двух поверхностей второго порядка позволила установить новые закономерности получения четыре – четырехзначных соответствий между двумя несовмещенными плоскостями. Разработанный на совмещенной плоскости метод получения биквадратичных преобразований плоскости, порождаемый бинарным отображением двух поверхностей второго порядка. Этот метод позволил получить двенадцать видов канонических биквадратичных преобразований плоскости. Кроме этого, разработанный алгоритм математической модели канонических биквадратичных преобразований плоскости, что необходимо для их практического применения.
В статье предлагается конструирование и новый способ построения поверхности туннеля в соответствии с предопределенными условиями с использованием биквадратичного преобразования плоскости, что позволяет описать конструкцию каждой секции туннеля на одно уравнение.
Для того, чтобы определить способ получения кривых с использованием биквадратичных преобразований, сечение поверхности туннеля может быть задано различными способами. В предлагаемом способе прообраз (кривая п) подвергается геометрическому преобразованию, в результате чего получается образ (искомая кривая п/). При этом прообраз задается уравнением
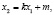
где k, m – постоянные коэффициенты.
Биквадратичное преобразование L8 задается уравнениями
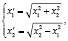
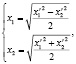
где х1/, х2/ – координаты точек образа; х1, х2 – координаты точек прообраза.
Уравнение полученной кривой п/ записывается в виде
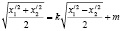 ,
,
где k, m – постоянные коэффициенты.
Для конструирования поверхности туннеля по заданным параметрам берем несколько точек прообраза п в соответствии, затем каждую из этих точек подвергаем преобразованию. Найдем множество точек, плавно соединив которые получим кривую образ п/. При этом форма кривой п/ зависит от значений коэффициентов m, k прообраза п.
Поверхность туннеля образуется в результате перемещения плоской кривой четвертого порядка (сечения) по оси направляющей кривой.
Результаты исследования и их обсуждение
Конструирование формы каналовой поверхности туннеля осуществляется, используя графическую модель биквадратичного преобразования следующими задачами:
Исходными данными для решения этой задачи являются осевая линия каналовой поверхности туннеля и законы изменения параметров поперечных сечений a и b. Каждое поперечное сечение п/ туннеля является кривой четвёртого порядка, полученной с использованием биквадратичного преобразования. При этом параметры a и b каждого поперечного сечения определяются из формул
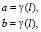 (5)
(5)
где l – расстояние от начала туннеля до рассматриваемого поперечного сечения.
Далее используем биквадратичное преобразование, задаваемое уравнением
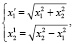 (6)
(6)
где 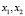 – координаты точки прообраза;
– координаты точки прообраза; 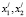 – координаты точки образа.
– координаты точки образа.
В качестве прообраза принимаем прямую линию общего положения п, уравнение которой имеет вид
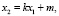 (7)
(7)
где k, m – постоянные коэффициенты.
Определяем коэффициенты k, m уравнения (7). Для этого используем свойства биквадратичного преобразования:
а) точка – прообраз В и точка – образ В2/ имеют одинаковую высоту. Точка В2/ является очерковой точкой сечения п/. Поэтому точка В прообраза п имеет координаты
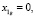 (8)
(8)
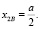 (9)
(9)
б) точка – прообраз С преобразуется в точки – образы С1/ = С3/ и С2/ = С4/, которые лежат на оси Ох1. Точка С1/ имеет координаты (b + c; 0). Точке С1/ соответствует точка С, координаты которой удовлетворяют условию
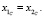 (10)
(10)
Из хода построения точки С1/ можно получить следующее уравнение:
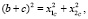 (11)
(11)
где с = a/2.
Таким образом, при выполнении условия уравнения (10), подставляя значение в уравнение (11), получим
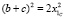 или
или 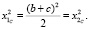 (12)
(12)
Через точки В и С проводим прообраз п и, учитывая это, составляем следующую систему уравнения:
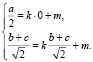 (13)
(13)
В результате решения данной системы уравнения получим значение m и k:
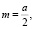 (14)
(14)
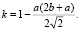 (15)
(15)
Для получения искомого сечения туннеля, которое удовлетворяет наперед заданным условиям, подвергаем прообраз п биквадратичному преобразованию. Алгебраическое уравнение этого сечения имеет вид
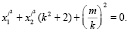 (16)
(16)
где k, m – параметры прообраза, описанные уравнениями (14) и (15).
Таким образом, параметрическое уравнение сечения туннеля имеет следующий вид:
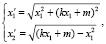 (17)
(17)
где х1 – параметры, 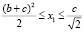 ;
; 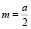 ;
; 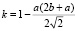 .
.
Полученное параметрическое уравнение можно применить при конструировании любого требуемого сечения рассматриваемой поверхности туннеля.
Заключение
Конструирование поверхности туннеля представляет собой сложную криволинейную поверхность, которая должна отвечать заданным требованиям, а конструкция поверхности туннеля требует значительных затрат времени. В результате исследований получен новый способ построения поверхности туннеля в соответствии с предопределенными условиями с использованием биквадратичного преобразования плоскости, что позволяет описать конструкцию каждой секции туннеля одним уравнением.
Таким образом, предлагаемый метод конструирования с использованием биквадратичного преобразования позволяет получить различные классы каналовых поверхностей и определить уравнение семейства поперечных сечений рассматриваемой поверхности, что облегчает дальнейшие геометрические расчеты на компьютере.
Библиографическая ссылка
Байдабеков А.К., Кемельбекова Э.А. БИКВАДРАТИЧНЫЕ ПРЕОБРАЗОВАНИЯ И КОНСТРУИРОВАНИЕ ТУННЕЛЕЙ // Международный журнал прикладных и фундаментальных исследований. – 2019. – № 1. – С. 43-46;URL: https://applied-research.ru/ru/article/view?id=12638 (дата обращения: 26.04.2024).

