Радиационно-стойкие материалы являются важными средствами для применения в термоядерных ректорах. Прогнозировать, т.е. моделировать кинетику диффузионно-управляемого накопления и термического отжига радиационно-индуцированных дефектов важно в рассмотрении современного понимания процессов термического отжига в твердых телах. В настоящее время твердо установлено, что в образовании, распаде и взаимопревращении радиационно-наведенных дефектов определенную роль играют подвижные ионные дефекты, образующиеся при радиационно-стимулированных и термостимулированных процессах в ионных кристаллах [1–4]. Радиационно образованные подвижные дефекты имеют конечную длину свободного пробега, поэтому для описания кинетики накопления и термического отжига дефектов рассмотривают различные подходы. В работах [5, 6] разработан и успешно применен теоретический подход, описывающих пространственное распределение сходных и разнородных дефектов, который позволяет изучать кинетику дефектов.
На основе детального исследования установлено, что процессы термического, фототермического отжига и тушения свечения радиационно-наведенных дефектов в щелочно-галоидных кристаллах имеют многостадийный характер. Однако кинетика и характер процессов, приводящих к многостадийному распаду радиационно-наведенных дефектов, теоретически обоснованы недостаточно.
Для моделирования многостадийного характера термического и фототермического отжига дефектов в твердых телах необходимо сперва остановить процесс отжига на определенной стадии процесса, затем надо приводить к отжигу дефектов в следующей стадии процесса.
В работах [7, 8], при использовании диффузионной теории рекомбинации, получены дифференциальные уравнения для отжига радиационных дефектов для коррелированной пары частиц. Генетически связанные, коррелированные между собой пары частиц характеризуются однокомпонентной парой N.
Однако некоррелированные, т.е. генетически не связанные между собой радиационно-наведенные центры и подвижные дефекты на основе вышеуказанной теории не рассмотрены.
Цель исследования: рассмотрение определения кинетики и механизмы термического отжига генетически не связанных некоррелированных дефектов в ионных кристаллах.
При этом было использовано дифференциальное уравнение для описания рекомбинации генетически не связанных между собой пар в следующем виде (центры окраски N и подвижные дефекты n). Для некоррелированных между собой рекомбинационных частиц каждый тип частиц характеризуется своей концентрацией N(t) и n(t).
Концентрации некоррелированных частиц можно теперь изменять различно, увеличивая одни и уменьшая другие. Тогда закономерности их рекомбинаций будут определяться от рекомбинации некоррелированных между собой частиц N и n. Поэтому для длительных релаксационных процессов имеют значение рекомбинации коррелированных или некоррелированных частиц.
Материалы и методы исследования
Исходя из представлений диффузионной теории рекомбинации для генетически не связанных между собой центров и подвижных диффузионных дефектов, многостадийные кривые термического отжига, происходящие по реакции первого порядка, получить не удалось.
Для решения этого вопроса в этом случае были использованы математические методы моделирования представления диффузионной теории рекомбинации, когда корреляция подвижных дефектов с концентрацией центров окраски данного типа происходит частично и взаимодействует так же, как генетически связанные, коррелированные пары.
Если N – концентрация всех распадающихся дефектов данного типа, а 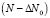 – концентрации центров коррелированных с дефектами-разрушителями, то после рекомбинации концентрация оставшихся центров – ΔN0. Если исчерпается концентрация центров N0 на концентрации
– концентрации центров коррелированных с дефектами-разрушителями, то после рекомбинации концентрация оставшихся центров – ΔN0. Если исчерпается концентрация центров N0 на концентрации 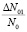 , то после первой стадии термического отжига процесс должен остановиться после первой стадии.
, то после первой стадии термического отжига процесс должен остановиться после первой стадии.
На основе диффузионной теории рекомбинации в работах [7, 8] предложено уравнение для скорости рекомбинации коррелированных пар 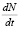 под действием частично коррелированных дефектов-разрушителей.
под действием частично коррелированных дефектов-разрушителей.
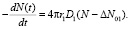 (1)
(1)
Для изотермических условий это уравнение имеет вид
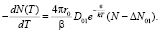 (2)
(2)
Решение этого дифференциального уравнения будет в следующим виде:
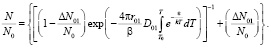 (3)
(3)
Тогда процесс, определяющийся этим выражением, приводит к распаду на первой стадии термического отжига и уменьшению относительной концентрации центров до 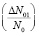 , так как второй сомножитель первого слагаемого уменьшается экспоненциально с ростом температуры и стремится к нулю. Кинетика этого процесса приведена на рис. 1.
, так как второй сомножитель первого слагаемого уменьшается экспоненциально с ростом температуры и стремится к нулю. Кинетика этого процесса приведена на рис. 1.
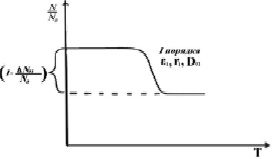
Рис. 1. Кинетика процесса
Для дальнейшего распада центров окраски, оставшихся после первой стадии ТО, необходимо дальнейшее действие ионов-разрушителей.
Результаты исследования и их обсуждение
Характер дальнейшего распада центров зависит от таких факторов, какие значения имеют величины ΔN01, т.е. от концентрации центров, оставшихся после первой стадии термического отжига дефектов.
Рассмотрим отдельные случаи:
1) Если ΔN01 – коррелированная пара центров и подвижных дефектов, тогда вторая стадия кинетики процесса термического отжига происходит по реакции первого порядка.
В этом случае для коррелированных пар центров окраски возможны два случая.
1а) Коррелируемые с центрами окраски дефекты-разрушители вызывают распад центров окраски на второй стадии ТО того же типа, что и у дефектов разрушителей, вызвавших распад центров окраски на первой стадии. Но дефекты-разрушители, вызывающие распад центров окраски на второй стадии, образуются в ходе релаксации.
В этом случае на оставшиеся концентрации центров окраски 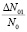 действуют коррелированные дефекты того же типа, но оставшиеся из комплементарных микродефектов. Они доведут эту коррелляцию до нуля, и термический отжиг доходит до конца. Тогда имеем двухстадийные кривые ТО, обе стадии которого происходят по реакции первого порядка.
действуют коррелированные дефекты того же типа, но оставшиеся из комплементарных микродефектов. Они доведут эту коррелляцию до нуля, и термический отжиг доходит до конца. Тогда имеем двухстадийные кривые ТО, обе стадии которого происходят по реакции первого порядка.
В этом случае кинетическое уравнение имеет следующий вид:
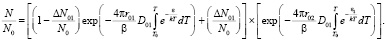 (4)
(4)
Вторая стадия ТО идет по реакции первого порядка до конца, некоррелированными дефектами того же типа, но образующейся из коррелированных дефектов образующихся в ходе релаксации, из комплементарных микродефектов (рис. 2, 1а случай).
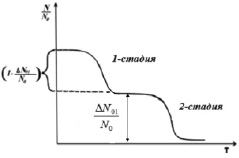
Рис. 2. Температурная зависимость относительной концентрации центров окраски для некоррелированных и коррелированных дефектов: 1а – случай: 1 – стадия: 1 – порядка; 2 – стадия: I – порядка; 1б – случай: 1 – стадия: 1 – порядка; 2 – стадия: I – порядка; 2а случай: 1 – стадия: 1 – порядка; 2 – стадия: II – порядка; 2б – случай: 1 – стадия: 1 – порядка; 2 – стадия: II – порядка; 2в – случай: 1 – стадия: 1 – порядка; 2 – стадия: II – порядка
1б) Коррелируемые с центрами данного типа дефекты-разрушители другого типа, чем те, которые вызывали распад центров окраски на первой стадии ТО, и имеют характеристики 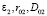 . В этом случае вторая стадия тоже происходит по кинетике первого порядка. На оставшиеся концентрации центров окраски
. В этом случае вторая стадия тоже происходит по кинетике первого порядка. На оставшиеся концентрации центров окраски 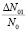 действуют коррелированные дефекты-разрушители другого типа:
действуют коррелированные дефекты-разрушители другого типа: 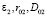 . Тогда также имеем двухстадийную кривую, в которой обе стадии происходят по кинетике первого порядка (рис. 2, 1б случай).
. Тогда также имеем двухстадийную кривую, в которой обе стадии происходят по кинетике первого порядка (рис. 2, 1б случай).
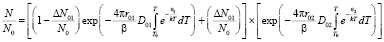 (5)
(5)
2) Если 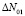 – некоррелированная пара центров и дефектов-разрушителей, тогда вторая стадия ТО протекает по реакции второго порядка. В случае для некоррелированных пар центров и дефектов-разрушителей возможны три случая.
– некоррелированная пара центров и дефектов-разрушителей, тогда вторая стадия ТО протекает по реакции второго порядка. В случае для некоррелированных пар центров и дефектов-разрушителей возможны три случая.
2а) Некоррелированными дефектами являются дефекты того же типа, что и вызвали распад центров на первой стадии термического отжига, но разлетевшиеся от центра данного типа на более далекие расстояния, чем дефекты-разрушители, вызвавшие первую стадию.
В этом случае на оставшиеся концентрации центров 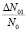 действуют некоррелированные дефекты того же типа, что и вызвавшие первую стадию, но разлетевшиеся друг от друга более далекие расстояния (рис. 2, 2а случай). Тогда имеем
действуют некоррелированные дефекты того же типа, что и вызвавшие первую стадию, но разлетевшиеся друг от друга более далекие расстояния (рис. 2, 2а случай). Тогда имеем
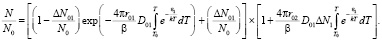 (6)
(6)
2б) Некоррелированными дефектами являются дефекты того же типа, что и те, которые вызвали распад центров данного типа на первой стадии ТО, но которые образуются от микродефектов, некоррелированных с центрами, имеющими очень большую концентрацию. Тогда вторая стадия ТО, образующаяся от некоррелированных дефектов большой концентрации, идет по реакции второго порядка.
В этом случае на оставшиеся концентрации центров окраски действуют некоррелированные дефекты того же типа, образующиеся в ходе релаксации, отщепленные от некоррелированных микродефектов, концентрации которых достаточно большие (рис. 2, 2б случай). Тогда имеем
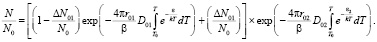 (7)
(7)
2в) Некореллированными дефектами являются дефекты другого типа, чем те, которые привели к первой стадии ТО и имеют характеристики 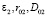 . В этом случае на оставшиеся концентрации центров действуют некоррелированные пары дефектов другого сорта. Тогда имеем
. В этом случае на оставшиеся концентрации центров действуют некоррелированные пары дефектов другого сорта. Тогда имеем
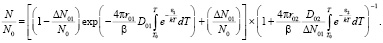 (8)
(8)
В этом случае вторая стадия ТО происходит по кинетике второго порядка до конца, некоррелированными дефектами другого типа, чем на стадии первой стадии термического отжига (рис. 2, 2в случай).
Заключение
Из вышеизложенных данных следуют выводы:
1. Получены кинетические уравнения и их решения для изотермического случая, для коррелированных и некоррелированных пар рекомбинационных дефектов в ионных кристаллах. Кинетика и механизм термического распада радиационных дефектов определяется коррелированностью с центрами окраски подвижных дефектов и соотношениями между начальными концентрациями радиационных центров и подвижных диффузионных дефектов.
2. Коррелируемые с центрами окраски подвижные дефекты, вызывавщие распад на второй стадии того же типа, что и у дефектов-разрушителей, вызвавших распад на первой стадии, но образующейся в ходе релаксации, тогда обе стадии распада радиационных дефектов происходят по реакции первого порядка.
3. Если подвижные дефекты другого сорта, чем тех дефектов которые вызывали распад центров окраски на первой стадии, однако коррелируемые с центрами окраски, тогда вторая стадия распада радиационных дефектов также происходит по кинетике первого порядка.
4. Если подвижные диффузионные дефекты, вызвавщих термический распад во второй стадии некоррелированы с центрами окраски, тогда вторая стадия распада радиационных дефектов происходит по кинетике второго порядка.
Библиографическая ссылка
Арапов Б.А., Арапов Т.Б., Орозбаева А.А. МОДЕЛИРОВАНИЕ КИНЕТИКИ РАСПАДА РАДИАЦИОННО-НАВЕДЕННЫХ ДЕФЕКТОВ В ИОННЫХ КРИСТАЛЛАХ // Международный журнал прикладных и фундаментальных исследований. – 2020. – № 2. – С. 115-119;URL: https://applied-research.ru/ru/article/view?id=13021 (дата обращения: 25.04.2024).

