Высокотемпературные сверхпроводники все чаще рассматриваются в качестве перспективных материалов для создания обладающих малыми потерями устройств фотоники и микроэлектроники. Наличие у высокотемпературных сверхпроводников очень малого сопротивления при температурах ниже критической уменьшает диссипацию энергии и увеличивает быстродействие устройств на их основе. Большое распространение нашли тонкопленочные сверхпроводящие устройства [1]. Отличительной особенностью высокотемпературных сверхпроводников является наличие смешанного состояния, в котором магнитное поле может проникать в сверхпроводник [2]. При этом при протекании транспортного тока в сверхпроводнике возникает проблема термомагнитной неустойчивости сверхпроводящего состояния, обусловленная дополнительной диссипацией энергии из-за наличия омических потерь. Термомагнитная неустойчивость приводит к скачкам магнитных свойств сверхпроводника вблизи критической температуры, что может приводить к переходу из сверхпроводящего состояния в обычное при любых сколь угодно малых внешних воздействиях [3]. Если же использовать высокотемпературные сверхпроводники в виде тонких пленок на подложке, то такая конструкция способствует отводу дополнительного тепла и уменьшает термомагнитную неустойчивость [3, 4]. В настоящей работе рассматриваются электродинамические свойства тонкой пленки высокотемпературного сверхпроводника в резистивном состоянии, находящейся на диэлектрической подложке. В резистивном состоянии магнитное поле, величина которого не превышает второе критическое поле, проникает в толщу сверхпроводящей пленки в виде упорядоченной структуры несверхпроводящих нитей, которая получила название решетки вихрей Абрикосова. Цилиндрические вихри Абрикосова ориентируются вдоль внешнего магнитного поля и составляют упорядоченную структуру. При увеличении температуры при Т > 0 из-за тепловых флуктуаций вихри будут отклоняться от положения равновесия и упорядоченная решетка вихрей начинает «плавиться». Такая же картина наблюдается при протекании транспортного тока по пленке из-за влияния силы Лоренца. В настоящее время существует несколько моделей, которые описывают поведение вихревой структуры в сверхпроводнике при температурах, приближающихся к критической. Среди них можно назвать XY-модель, модель взаимодействия двухмерных бозонов, модель замкнутых вихрей [2]. В данной работе для описания свойств вихревой жидкости используется модель динамической магнитной восприимчивости [5].
Материалы и методы исследования
Геометрия структуры изображена на рис. 1. Слой № 1 – высокотемпературный сверхпроводник толщиной d1, слой № 2 – диэлектрик толщиной d2. Структура находится в магнитном поле В, направленном перпендикулярно границе раздела слоев. Величина магнитного поля не превышает второго критического поля для сверхпроводника Bc2. Тонкая пленка высокотемпературного сверхпроводника находится в смешанном состоянии. В режиме смешанного состояния магнитное поле проникает в сверхпроводящую пленку в виде решетки вихрей Абрикосова, и высокотемпературный сверхпроводник приобретает слабые магнитные свойства [6]. Электромагнитная волна падает на рассматриваемую структуру под углом q.
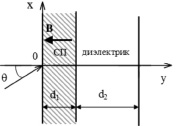
Рис. 1. Геометрия структуры
Для расчета магнитных свойств тонкой сверхпроводящей пленки рассмотрим модель динамической магнитной восприимчивости, которая учитывает возможность изменения параметров вихрей Абрикосова. Будем исследовать случай «вихревой жидкости», которая демонстрирует линейный отклик решетки вихрей Абрикосова на малое внешнее возмущение. В рамках рассматриваемой модели магнитная восприимчивость тонкой сверхпроводящей пленки рассчитывается по формуле [6]:
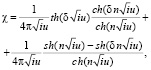(1)
где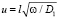 
– безразмерный параметр, D = c2/(4prv) – коэффициент диффузии, 2l – ширина образца, 
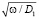– характерная длина диффузии, d = d/l – доля объема образца, занятого так называемой внутренней областью, rv – удельное линейное сопротивление, обусловленное движением вихрей, 
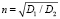– коэффициент нелинейности вольт-амперной характеристики сверхпроводника, который связан с величиной коэффициентов диффузии D1 и D2.
Магнитная проницаемость образца рассчитывается по формуле
μ = 1 + χ. (2)
Мы рассматриваем высокотемпературный сверхпроводник в смешанном состоянии, которое возникает в том случае, если магнитном поле, которое приложено к сверхпроводящей пленке, находится в следующих пределах: Bc1 < B < Bc2, где Bc1 – первое критическое поле, Bc2 – второе критическое поле для сверхпроводника. При этом внутри сверхпроводящей тонкой пленки из магнитных вихрей формируется упорядоченная решетка вихрей Абрикосова. Причем магнитные свойства будут зависеть как от внешнего магнитного поля, температуры, так и от соотношения характерных времен тепловых и электромагнитных процессов в сверхпроводящей пленке, а также, опосредованно, и от характерных размеров сверхпроводника [2].
В данной работе исследуется, как зависят электродинамические параметры сверхпроводящей тонкой пленки от величины внешнего магнитного поля В. Рассмотрим случай однородной и изотропной пленки сверхпроводника в параллельном магнитном поле. Зависимость удельной проводимости для тонких пленок из высокотемпературной иттриевой керамики в слабых магнитных полях была исследована в работе [6]. Для однородного сверхпроводника второго рода удельная проводимость находится из решения уравнения Гинзбурга – Ландау. При этом зависимость удельной проводимости от величины внешнего магнитного поля описывается выражением [7]:
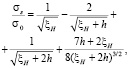(3)
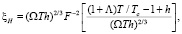
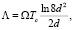
где h = B/Bc2(0) – магнитное поле, отнесенное к величине Bc2(0), Bc2(0) – второе критическое поле для сверхпроводника при температуре T = 0 К, xH – выполняет роль безразмерной температуры, s0 – константа с размерностью удельной проводимости, d = s/2xc(0), s – расстояние между CuO плоскостями, xс(0) – корреляционная длина в направлении, перпендикулярном плоскости CuO иттриевой керамики, xab(0) – корреляционная длина в направлении плоскости CuO иттриевой керамики.
Величина Ω принимает следующие значения:
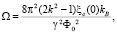(4)
где g = xс(0)/ xab(0) – параметр анизотропии, Ф0 – квант магнитного потока, k – параметр Гинзбурга – Ландау, F(x) – некоторая функция, удовлетворяющая кубическому уравнению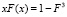 
.
Результаты исследования и их обсуждение
Рассмотрим влияние магнитного поля на электродинамические свойства тонкой пленки высокотемпературного проводника при высоких частотах. Расчет коэффициента отражения от структуры сверхпроводящая пленка – диэлектрическая подложка проводился с использованием матричного метода. Матрица преобразования для слоя диэлектрика известна (см. работу [8]), матрица преобразования для тонкой пленки сверхпроводника приведена в работе [9]. Результаты расчета зависимости модуля коэффициента отражения рассматриваемой структуры от магнитного поля представлены на рис. 2. Параметры, использованные для расчета: толщина сверхпроводящей пленки d1 = 25 нм, толщина диэлектрической подложки d2 = 0,25 мкм, диэлектрическая проницаемость подложки e2 = 9,8, угол падения на структуру q = 0,1, a = 20, g = 2, sn(1) = 3,5×106 См/м, l(0) = 0,13 мкм, Тс = 89 К, d = 0,7.
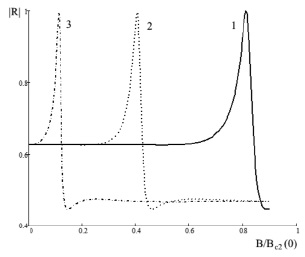
Рис. 2. График зависимости модуля коэффициента отражения от двухслойной структуры тонкая сверхпроводящая пленка – диэлектрик от величины магнитного поля B/Bc2(0) для разных температур. Кривая 1: t = 0,56, кривая 2: t = 0,7, кривая 3: t = 0,8, частота ω = 1012 рад/с
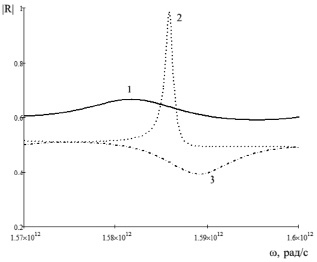
Рис. 3. График зависимости модуля коэффициента отражения от двухслойной структуры сверхпроводник – диэлектрик от частоты для разных значений температуры. Кривая 1: t = 0,5, кривая 2: t = 0,52, кривая 3: t = 0,55, h = 0,3
Из рис. 2 видно, что коэффициент отражения от тонкой сверхпроводящей пленки на диэлектрической подложке существенным образом зависит как от магнитного поля, так и от температуры. Причем при увеличении температуры максимум коэффициента отражения наблюдается при более низких магнитных полях. На рис. 3 показан результат расчета частотной зависимости модуля коэффициента отражения от рассматриваемой структуры для разных значений температуры, а на рис. 4 представлена частотная зависимость модуля коэффициента отражения для разных значений величины внешнего магнитного поля. Параметры структуры те же, что и на рис. 2.
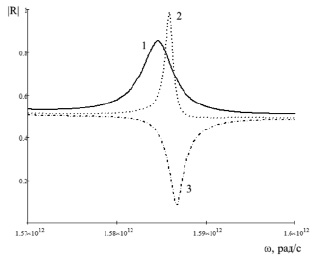
Рис. 4. График зависимости модуля коэффициента отражения от двухслойной структуры сверхпроводник – диэлектрик от величины частоты для разных значений магнитного поля h = B/Bc2(0). Кривая1: h = 0,27, кривая 2: h = 0,3, кривая 3: h = 0,31; t = 0,52
Из рис. 3 и 4 видно, что при соответствующем выборе величины магнитного поля и температуры коэффициент отражения R демонстрирует резкий максимум, причем в максимуме величина R практически равна единице (кривая 2 на обоих рисунках). Равенство единице коэффициента отражения при определенной частоте говорит о том, что на данной частоте электромагнитная волна не может распространяться в исследуемой структуре. Как показано в работе [10], вблизи данной частоты существует область, в которой электромагнитная волна полностью проходит через тонкую пленку сверхпроводника. Нахождение этой области аналитическими методами является весьма сложным и требует численного подбора всех параметров сверхпроводника, включая величину внешнего магнитного поля, температуру, угол падения и толщину.
Выводы
Таким образом, в работе показано, что тонкие пленки сверхпроводника второго рода, находящиеся во внешнем магнитном поле, могут демонстрировать достаточно сильные магнитные свойства, наблюдаемые для СВЧ-диапазона, а также при более высоких частотах. Использование ферромагнитной подложки повышает магнитный отклик тонких сверхпроводящих пленок. Наличие резкой зависимости коэффициента отражения от величины внешнего магнитного поля и температуры означает, что рассматриваемая двухслойная структура из тонкой сверхпроводящей пленки и слоя диэлектрика может служить высокоэффективным фильтром, полоса пропускания которого меняется под воздействием магнитного поля. Причем соответствующий подбор параметров, включающих температуру и толщину сверхпроводника, позволяет получить устройство с очень высокой чувствительностью.
Библиографическая ссылка
Головкина М.В. МЕТОДЫ УПРАВЛЕНИЯ КОЭФФИЦИЕНТОМ ОТРАЖЕНИЯ ОТ ТОНКОЙ СВЕРХПРОВОДЯЩЕЙ ПЛЕНКИ // Международный журнал прикладных и фундаментальных исследований. – 2020. – № 2. – С. 120-124;URL: https://applied-research.ru/ru/article/view?id=13022 (дата обращения: 19.04.2024).