Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ван Диен Хуа 1 Гаврикова Н.Ю. 2 Носкова Н.С. 1

---

1 Тяньцзиньский университет науки и технологий

2 Иркутский государственный университет путей сообщения

Настоящая статья посвящена исследованию закономерностей функционирования и развития российского продовольственного рынка с помощью аппарата математического моделирования, конкретно, регрессионного анализа. Продовольственный рынок при этом описывается тринадцатью переменными. В результате проведенного «конкурса» регрессионных уравнений получена математическая модель продовольственного рынка России, включающая в себя восемь взаимосвязанных регрессионных нелинейных зависимостей, обладающих высокими значениями критериев адекватности – детерминации, Фишера, Стьюдента, средней относительной ошибки аппроксимации.

Статья в формате PDF

765 KB

продовольственный рынок

математическая модель

регрессионный анализ

конкурс моделей

критерии адекватности

1. Носков С.И. Технология моделирования объектов с нестабильным функционированием и неопределенностью в данных. – Иркутск, 1996. – 320 с.

2. Федеральная служба государственной статистики РОССТАТ [электронный ресурс] // gks.ru. (дата обращения 08.08.2014).

3. Матросов В.М., Головченко В.Б., Носков С.И. Моделирование и прогнозирование показателей социально-экономического развития области. – Новосибирск: наука, 1991. – 144 с.

4. Носков С.И. Коррекция параметров регрессионных уравнений по критерию «согласованности поведения» // Кибернетика и системный анализ. – 1994. – № I. – С. 177–180.

5. Носков С.И., Потороченко Н.А. Диалоговая система реализации «конкурса» регрессионных моделей // Управл. Системы и машины. – 1992. – № 2–4. – С. 111–116.

6. Носков С.И., Потороченко Н.А. Об одном подходе к организации «конкурса» эконометрических моделей // Всес. Конф. «Территориальные неоднородные информационно-вычислительные системы». Тезисы докл. – Новосибирск, 1988. – С. 94–96.

7. Базилевский М.П., Носков С.И. Методические и инструментальные средства построения некоторых типов регрессионных моделей // Системы. Методы. Технологии. – Братск, 2012. – № 1(13). – С. 80–87.

8. Базилевский М.П., Носков С.И. Программный комплекс автоматизации процесса построения регрессионных моделей (Program complex for automation construction process of regression models) // Свидетельство о государственной регистрации программы для ЭВМ № 2010617199.

9. Базилевский М.П., Носков С.И. Технология организации конкурса регрессионных моделей // Информационные технологии и проблемы математического моделирования сложных систем. – Иркутск, 2009. – Вып. 7. – С. 77–84.

Как известно [1], методы математического моделирования являются признанным инструментом научного анализа сложных, с множеством внутренних и внешних взаимосвязей, объектов различной природы. Они позволяют на модельном уровне формализовывать закономерности, присущие этим объектам, посредством разработки их качественных абстрактных образов, что открывает широкие возможности в повышении эффективности вырабатываемых управляющих воздействий, поскольку при том экспериментирование может проводиться не с «живой» системой а с ее математической моделью.

Прикладная значимость этих методов весьма высока. Он давно и успешно используются в различных отраслях знаний, во многом способствуя лучшему пониманию изучаемых процессов. Традиционно одно из наиболее широких средств применения методов математического моделирования является экономика, которая в силу своей специфики особенно активно и плодотворно потребляет новые достижения, появляющиеся в этой области.

Целью настоящей работы является формализация с помощью методов математического моделирования взаимосвязей факторов, определяющих продовольственный рынок. Мы выделили 13 таких факторов:

Х1 – производство мяса (млн тонн);

Х2 – производство зерна (млн тонн);

Х3 – производство молока (тыс. тонн);

Х4 – потребление продуктов питания на душу населения;

Х5 – стоимость 1 кг говядины;

Х6 – стоимость 1 кг свинины;

Х7 – стоимость 1 кг хлеба;

Х8 – стоимость 1 кг пшеничной муки;

Х9 – стоимость 1 л молока;

Х10 – стоимость минимального набора продуктов (руб.);

Х11 – объем импорта мяса (тыс. тонн);

Х12 – объем импорта зерна (млн тонн);

Х13- объем импорта молока (тыс. тонн);

Была собрана статистическая информация о значениях этих показателей за 2000-2013 годы (сайт РОССТАТа [2]). Эти данные приведены в таблице.

В качестве метода моделирования был использован один из основных разделов анализа данных – регрессионный анализ, прикладные аспекты которого изложены, в частности, в работе 1. В соответствии с методологией регрессионного анализа, все перечисленные факторы(показатели, переменные) были разбиты на две группы – выходные (внутренние, зависимые, эндогенные) и входные ( внешние, независимые, экзогенные). В первую группу вошли факторы: Х4, Х5, Х6, Х7, Х8, Х9, Х10, Х11, Х12, Х13, остальные показатели составили вторую группу. При этом допускалось, что в одних уравнениях одна и та же переменная являлась выходной, а для других уравнений – входной.

Статистические данные показателей рынка продовольствия Российской Федерации

Одним из основных достоинств регрессионного анализа является наличие в нем хорошо обоснованных частных характеристик адекватности модели. Мы в нашей работе будем использовать 4 таких критерия: R – критерий множественной детерминации, указывающей на то, какой процент значимых независимых переменных включен в уравнение; F – критерий Фишера, указывающий на значимость предыдущего критерия; E – средняя относительная ошибка аппроксимации, не требующая дополнительных пояснений; ti – критерий студента, указывающий на значимость i-го фактора. Часть этих критериев при использовании требует привлечения статистических таблиц соответствующего распределения. В практике же моделирования, при создании конкретных моделей реальных объектов, принято использовать такие величины(смотрите в частности монографию [3]):

R > 0,9;

F > 12;

E < 10;

Ti > 1;

Ниже приведены полученные восемь уравнений модели и указаны значения критериев их адекватности.

.

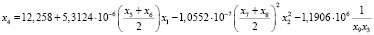Критерии адекватности:

R = 0,98803, F = 206,33, E = 1,7581 %,

t0 = 11,58, t1 = 9,254, t2 = – 1,812, t3 = – 3,156

.

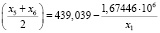Критерии адекватности:

R = 0,96406, F = 160,93, E = 8,8153 %,

t0 = 26,39, t1 = – 17,94

.

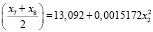Критерии адекватности:

R = 0,9070, F = 78,71959, E = 6,063 %,

,

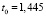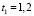
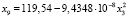
Критерии адекватности:

R = 0,9709, F = 92,2293, E = 8,703 %,

,

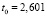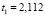
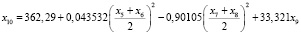
Критерии адекватности:

R = 0,98187, F = 135,4, E = 5,5719 %,

t0 = 2,169, t1 = 5,114, t2 = – 2,685, t3 = – 2,121

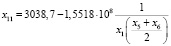
Критерии адекватности:

R = 0,8889, F = 32,4384, E = 7,479 %,

,

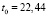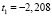
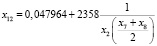
Критерии адекватности:

R = 0,8994, F = 28,978, E = 10,595 %,

,

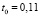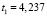
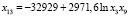
Критерии адекватности:

R = 0,87972, F = 43,884, E = 5,7659 %,

, .

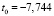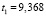При построении каждого уравнения модели проводился так называемый конкурс моделей, состоящий в разработке множества альтернативных вариантов модели и выделении из них наилучшего на основе применения соответствующих методов векторной оптимизации, таких, например, как методы идеальной точки, уступок, взвешивание критериев. Научные основы проведения такого конкурса представлены, в частности, в работах [4–6]. В число альтернативных вариантов уравнения входили в том числе существенно нелинейные варианты, в математическом отношении представляющие собой аддитивные функции.

Технологической основой проведения такого конкурса стал программный комплекс автоматизации процесса построения регрессионных моделей (ПК АППРМ [7–9]). Анализ приведенной модели позволяет выявить закономерности формирования и развития рынка продовольствия России. Так, в соответствии с 5-м уравнением, стоимость минимального набора продуктов с высокой точностью определяется квадратом средней цены говядины и свинины, средней стоимости произведенных хлеба и муки, а так же стоимостью молока. Этот набор показателей в правой части на 98 % определяет стоимость минимального набора продуктов. Если же взять последнее, 8-е уравнение, можно видеть, что объем импорта молока на 87 % определяется логарифмом произведения объема произведённого молока и его стоимости. На корректность такого анализа указывают высокие значения критериев адекватности для всех восьми уравнений. Кроме того, эта модель позволяет проводить кратко- и среднесрочное прогнозирование перечисленных выше выходных переменных. В своих последующих работах авторы намерены продолжить изучение рынка продовольствия России путем, в частности, усовершенствования данной модели.

Библиографическая ссылка