Разработка корректных методов решения обратной задачи – получения термодинамической информации из фазовой диаграммы квазибинарных систем, составленных из немолекулярных соединений, является весьма актуальной задачей. Такая термодинамическая информации, взаимосогласованная с фазовой диаграммой граничных квазибинарных систем, позволяет вычислить фазовую диаграмму и термодинамические функции квазитройных и более сложных систем при использовании малого числа экспериментальных данных [1, 2].
Неорганические полупроводники, в частности теллуриди металлов, а также сурьмы и висмута относятся к немолекулярным соединениям. Эти соединения образуют квазибинарные, квазитройные и более сложные соединения. В работах [1–3] показано, что для преобразования термодинамических уравнений применительно к системам полупроводниковых соединений вместо мольной доли компонентов следует использовать функции f(x), учитывающих конкретную формулу соединения:
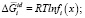
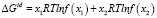 (1)
(1)
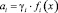 (2)
(2)
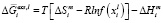 (3)
(3)
В уравнениях (1–3): 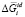 – парциальная мольная свободная энергия смешения Гиббса компонента i в идеальном растворе,
– парциальная мольная свободная энергия смешения Гиббса компонента i в идеальном растворе, 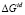 – интегральная мольная свободная энергия смешения Гиббса; Т-температура по линии ликвидуса, х – моль доля, аi – термодинамическая активность, γi – коэффициент активности,
– интегральная мольная свободная энергия смешения Гиббса; Т-температура по линии ликвидуса, х – моль доля, аi – термодинамическая активность, γi – коэффициент активности, 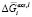 – парциальная мольная избыточная свободная энергия смешения Гиббса компонента i в жидком растворе по линии ликвидуса,
– парциальная мольная избыточная свободная энергия смешения Гиббса компонента i в жидком растворе по линии ликвидуса, 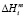 – мольная энтальпия плавления соединения i,
– мольная энтальпия плавления соединения i, 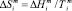 – мольная энтропия плавления,
– мольная энтропия плавления, 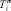 – температура плавления соединения i, функция f(x) включает стехиометрические коэффициенты компонентов квазибинарной системы [2]. В частности, для квазибинарной системы типа ApBq – CmBn:
– температура плавления соединения i, функция f(x) включает стехиометрические коэффициенты компонентов квазибинарной системы [2]. В частности, для квазибинарной системы типа ApBq – CmBn:
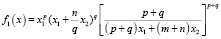 . (4)
. (4)
Здесь x1; x2 – моль доли соединений ApBq – CmBn. Формулы типа (4) существенно упрощаются для конкретных систем. Для квазибинарной системы типа АВ-СВ функция f(x) = х.
Формулы для функции f(x) нами использованы в ряде работ [5, 6] для расчета диаграмм состояний квазитройных и взаимных полупроводниковых систем. Однако к настоящему времени термодинамические уравнения квазибинарных систем в недостаточной степени апробированы для решения обратной задачи – расчета термодинамических величин на основании диаграмм состояния.
В этой работе термодинамические уравнения немолекулярных соединений апробируются на квазибинарной системе теллурид иттербия (II) – теллурид висмута(III), фазовая диаграмма которой определена в работе [7]. Выбор этой системы для термодинамического анализа связан тем, что соединение Bi2Te3 и фазы на их основе широко применяются в качестве термоэлектрических материалов [4], являются топологическими изоляторами и могут быть использованы в спинтронике и в квантовом компьютинге [8, 9].
Термодинамические расчеты. Фазовая диаграмма системы теллурид иттербия (II) – теллурид висмута (III)
Эта квазибинарная система может быть представлена в трех вариантах: YbTe-Bi2Te3, 0.5YbTe–Bi0.4Te0.6 и YbTe–BiTe1.5. Первый способ представления соединений с целочисленными индексами наиболее широко распространен. Во втором способе система нормируется к одному моль-атом. Этот вариант используется в программах компьютерного конструирования фазовых диаграмм [10]. Третий вариант будем использовать для сравнительного анализа.
При пересчете концентраций применительно к системам 0.5YbTe–Bi0.4Te0.6 и YbTe–BiTe1.5 кривые ликвидуса смешаются в сторону теллурида висмута(III) (рис. 1). Для пересчета концентраций использованы следующие формулы:
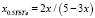
в системе 0.5YbTe–Bi0.4Te0.6 (5)
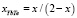
в системе YbTe–BiTe1.5 (6)
В уравнениях (5, 6) х – моль доли YbTe в системе YbTe-Bi2Te3.
Практически во всех работах по термодинамическому моделированию фазовых диаграмм, включая программы CALPHAD (в этих программах термодинамические функции нормируются к одному моль-атом) не учитываются значения индексов соединения в аналитических выражениях идеальных растворов [10]. В частности уравнения (1-3) используют в виде, где f(x) = х.
Формула (4) для первого компонента (теллурида иттербия) применительно к системам YbTe-Bi2Te3, 0.5YbTe–Bi0.4Te0.6 и YbTe–BiTe1.5, соответственно, имеет выражения:
f1(x) = (12x – 8x2)/(5 – 3x)2 (7)
f2(x) = (1.2x – 0.2x2)1/2 (8)
f3(x) = (6x-2x2)/(2.5 – 0.5x)2 (9)
Здесь х – моль. доля первого компонента в соответствующей квазибинарной системе. Вставляя формулы (7–9) в уравнение (3), вычислены значения парциальной мольной избыточной свободной энергии Гиббса теллурида иттербия. Термодинамическая активность теллурида иттербия вычислена по уравнению:
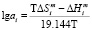 . (10)
. (10)
В уравнениях (3) и (10): 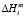 = 35600 Дж моль-1 энтальпия плавления YbTe. Эта величина нами определена расчетным путем двумя независимыми методами на основании теплоты плавления иттербия и теллура;
= 35600 Дж моль-1 энтальпия плавления YbTe. Эта величина нами определена расчетным путем двумя независимыми методами на основании теплоты плавления иттербия и теллура;
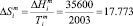 Дж моль-1К-1
Дж моль-1К-1
мольная энтропия плавления YbTe. Вставляя эти величины в уравнение (10) можем написать:
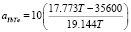 . (11)
. (11)
Применительно к системе 0.5YbTe–Bi0.4Te0.6 уравнение (11) имеет вид:
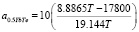 (12)
(12)
Результаты расчета с использованием уравн. (2, 3, 7–9, 11, 12) приведены в таблице и на рис. 2, 3.
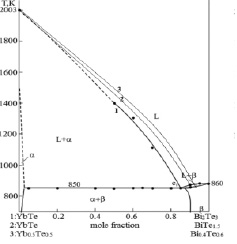
Рис. 1. Фазовая диаграмма системы теллурида иттербия (II) и теллурида висмута (III) в вариантах: 1 – YbTe-Bi2Te3 [7], 2 – YbTe–BiTe1.5 и 3 – 0.5YbTe–Bi0.4Te0.6
Значения температур ликвидуса, моль доли теллурида иттербия и функции f(x) в системах YbTe(1)-Bi2Te3(2); 0.5YbTe(1)-Bi0.4Te0.6(2); YbTe*(1)-BiTe1.5(2)
|
хYbTe |
х0.5YbTe |
хYbTe* |
T,K |
х |
f1(x) |
f2(x) |
f3(x) |
aYbTe |
|
0.100 |
0.0425 |
0.0512 |
0.1 |
0.0507 |
0.345 |
0.0966 |
– |
|
|
0.148 |
0.0650 |
0.0780 |
850 |
0.2 |
0.1074 |
0.481 |
0.1944 |
0.096 |
|
0.2 |
0.0909 |
0.1111 |
956 |
0.3 |
0.1712 |
0.575 |
0.2933 |
0.1956 |
|
0.3 |
0.1463 |
0.1765 |
1136 |
0.4 |
0.2348 |
0.670 |
0.3931 |
0.2989 |
|
0.4 |
0.2150 |
0.2500 |
1280 |
0.5 |
0.3280 |
0.742 |
0.4938 |
0.3982 |
|
0.5 |
0.2857 |
0.3330 |
1400 |
0.6 |
0.4203 |
0.805 |
0.5951 |
0.5107 |
|
0.6 |
0.3750 |
0.4286 |
1524 |
0.7 |
0.5340 |
0.865 |
0.6966 |
0.6309 |
|
0.7 |
0.4828 |
0.5385 |
1648 |
0.8 |
0.6639 |
0.917 |
0.7982 |
0.7526 |
|
0.8 |
0.6154 |
0.6667 |
1768 |
0.9 |
0.8151 |
0.961 |
0.8996 |
0.8779 |
|
0.9 |
0.7826 |
0.8181 |
1888 |
1.0 |
1 |
1 |
1 |
1 |
|
1.0 |
1.0 |
1.0 |
2003 |
Результаты исследования и их обсуждение
Из таблицы следует, что значения f1(x) и f2(x) для систем YbTe-Bi2Te3, 0.5YbTe–Bi0.4Te0.6 существенно отличаются от значений моль доли компонента х. Поэтому значения парциальной избыточной свободной энергии смешения теллурида иттербия согласуется с фазовой диаграммой только при учете состава соединений с помощью функций (7,8). Фазовая диаграмма системы теллурид иттербия (II) – теллурид висмута(III) состоит из ликвидуса кристаллизации YbTe и твердых растворов на основе Bi2Te3. Для такой системы характерно умеренное отклонение от идеальности, что наблюдается при использовании функций (7, 8): рис. 1, кривая 1 и рис. 2, кривые 2,3. При использовании же широко распространенных уравнений (1–3) с упрощением f(x) = х, расчетные данные противоречат характеру фазовой диаграммы: рис. 1, кривая 2 и рис. 2, кривые 1,5. В то же время, в системе YbTe–BiTe1.5, которая несмотря на то, что имеет непростую формулу (9), значения функции f3(x) практически совпадают с значениями моль доли компонента х. Эта связана с тем, что эта система относится к типу АВ–СВq, в которой индексы одноименных атомов практически не влияют на значения функции f(x). Поэтому для термодинамического моделирования подобных систем могут быть использованы уравнения (1–3) с упрощением f(x) = х.
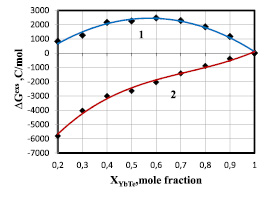
Рис. 2. Зависимости парциальной избыточной свободной энергии смешения теллурида иттербия для жидких сплавов по линии ликвидуса системы YbTe-Bi2Te3: 1 – расчет по уравнению (3, 7), аппроксимировано полиномом 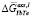 = –12830x2 + 14701x – 1762; 2 – расчет по уравнению (3), где f(x) = х, аппроксимировано полиномом
= –12830x2 + 14701x – 1762; 2 – расчет по уравнению (3), где f(x) = х, аппроксимировано полиномом 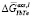 = 14636x3 – 32022x2 + 27501x – 10007
= 14636x3 – 32022x2 + 27501x – 10007
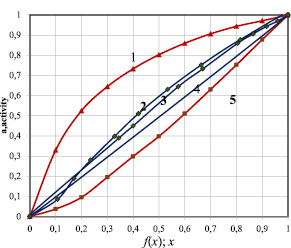
Рис. 3. Зависимость активности теллурида иттербия от состава для системы 0.5YbTe-Bi0.4Te0.6: 1–в виде а–х; 3–в виде a–f(x); для системы YbTe-Bi2Te3:2–в виде a–f(x); 5-в виде а–х, линия 4 относится к идеальному раствору
Следовательно, для термодинамического моделирования фазовой диаграммы квазибинарных систем типа ApBq – CmBn, включая систем, нормированных к одному моль атому, следует использовать уравнений вида (1–3), модифицированных с учетом состава соединений. Для систем типа ABq – CBn могут быть использованы уравнения (1–3) с упрощением f(x) = х.
Библиографическая ссылка
Мамедов А.Н., Расулова К.Д., Бабанлы М.Б. ТЕРМОДИНАМИЧЕСКИЕ УРАВНЕНИЯ РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ ФАЗОВЫХ РАВНОВЕСИЙ В СИСТЕМЕ ТЕЛЛУРИД ИТТЕРБИЯ – СЕСКВИТЕЛЛУРИД ВИСМУТА // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 8-5. – С. 869-873;URL: https://applied-research.ru/ru/article/view?id=7261 (дата обращения: 25.04.2024).

