Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гришкан Ю.С. 1

---

1 Южный федеральный университет

Показано, что можно построить точные решения уравнения Шрёдингера, обладающие определённым типом конформной симметрии. Эти решения удобно находить, как решения присоединённого к уравнению Шрёдингера уравнения Риккати. Выделен класс II точных решений. Найдены точные решения некоторых потенциалов, входящих в этот класс, в частности, для потенциала пространсвенного линейного гармонического осциллятора с вращением и для кулоновского потенциала в поле центробежных сил.

Статья в формате PDF

1583 KB

групповые методы

классы точных решений

уравнение Шрёдингера

1. Infeld L., Hall T.E. The factorization method // Reviews of modern Physics. – 1954 – v. 23, № 1. – P. 21–69.

2. Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нерелятивисткая теория. – М.: ГИТТЛ, 1963. – С. 1–700.

3. Флюгге З. Задачи по квантовой механике. – M: Мир, 1974. – С. 1–338.

4. Гришкан Ю.С., Усольцев О.А. Первый класс точно решаемых задач уравнений Шрёдингера квантовой механики. // Международный журнал прикладных и фундаментальных исследований. – 2016.

Поиск точных решений стационарного уравнения Шрёдингера является пограничной областью между физикой и математикой. Как правило, физикам известен очень ограниченный набор таких решений. Однако, такие решения могут быть найдены для многих систем электромагнитного и сильного взаимодействий, таких как молекулы, атомы и кварконии. Для поиска этих решений выделим несколько классов потенциалов, обладающих конформной симметрией, и найдём решения для этих классов. Затем, приспособим найденные решения к конкретным 2-х и 3-х параметрическим потенциалам квантовых систем, хорошо известных в физике электромагнитного и сильного взаимодействий.

Как известно [1], уравнение Шрёдингера в координатном представлении

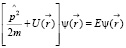(1)

после введения цепочки лестничных пары лестничных операторов

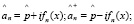
сводится к нелинейному операторному уравнению Риккати для операторной функции 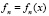в координатном представлении:

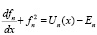. (2)

Цепочка операторов 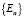образует спектр оператора Гамильтона

.

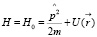Для простоты, не будем писать шляп над операторами.

Цепочка операторов 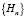факторизуется

.

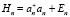Для нахождения спектра En рассмотрим одномерное и радиально-симметричное движение fn = fn(q).

Сведём радиально – симметричное движение к одномерному. Это делается с помощью перехода безразмерной координате 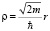[2]. В полный потенциал U(ρ) необходимо добавить центробежный член

.

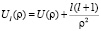Несложно показать, что радиальная часть волновой функции нормирована на единицу

,

, .

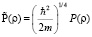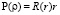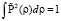Обозначив ρ = q, введём класс II точно решаемых задач для потенциалов

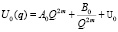, (3)

где 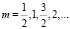, Q = Q(x) – некоторая функциональная форма, которую необходимо задать.

Будем искать точное решение уравнения (2) в виде

,

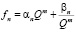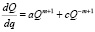, (4)

αn, βn – цепочки функций, подлежащих определению, a, c – известные константы.

Поставленная задача требует нахождения цепочек αn, βn, En, в виде функций констант A0, B0, U0, a, c.

Собирая коэффициенты при одинаковых степенях Q в уравнениях (3)-(4), получим следующие уравнения для неизвестных α0, β0, E0:

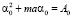
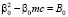
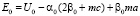(5)

Операторы цепочки 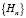находятся по рекуррентной формуле

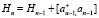(6)

Построим первый оператор цепочки (2)

.

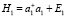Собирая коэффициенты при одинаковых степенях Q, построим систему уравнений для коэффициентов, подлежащих определению.

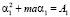
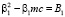
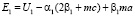(7)

где

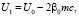
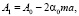
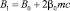
Для уравнений цепочки с индексом n получим

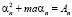
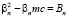
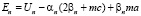(8)

Из (8) следуют тогда решения

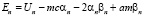, (9)

где

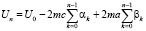
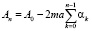(10)

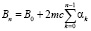
Решение уравнений (8), (9) даёт

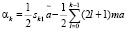(11)

где знак 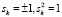устанавливается с учётом условий максимальности уровней энергии при факторизации,

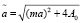. (12)

Также из (8), (9) следует

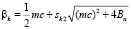(13)

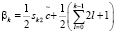, (14)

где

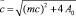(15)

Единый спектр существует при условиях на знаки

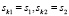(16)

Теперь можно получить решения для αn, βn выражения

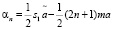(17)

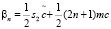(18)

С помощью (11), (14) получаем аналогичные выражения для сумм этих коэффициентов

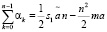(19)

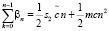(20)

После подстановки (19), (20) в (9) получим окончательное выражение для спектра системы

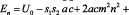
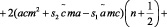
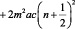. (21)

Рассмотрим две квантовые системы, относящиеся к классу II.

II-1. Кулоновский центробежный потенциал [2]

Пусть

m = 1, A0 = A0, B0 = B0, a = 0, c = 1. (22)

Тогда

Q = ρ. 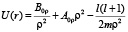. (23)

Этот потенциал изображён на рисунке при A0 = 5, B0 = 5, l = 0.

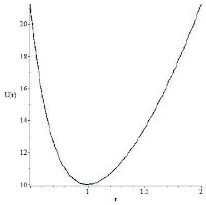
Кулоновский центробежный потенциал при А0ρ = B0ρ = 5, l = 0

Перейдём от безразмерных единиц расстояния ρ к физическим. Тогда

.

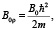
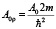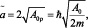
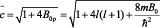. (24)

Спектр потенциала имеет вид

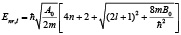. (25)

Последнее выражение совпадает с приведённым в [2] результатом.

II-1-1. Пусть

m = 1, ,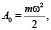

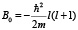a = 0, c = 1. (26)

Тогда Q = r,

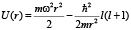. (27)

Спектр этого потенциала имеет вид

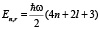. (28)

В теории линейного гармонического осциллятора величина n формулы (28) называется «радиальное квантовое число» обозначается nr [3] .Перепишем (28) через nr.

Главное квантовое число, пространственного осциллятора N = 2nr + l.

Спектр энергии

Пространственного осциллятора принимает тогда вид

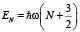, (29)

что совпадает с результатами, полученными в [2], [3].

Заключение

Классы точных решений I, II содержит более 20 точно решаемых потенциалов. Причём не для всех этих потенциалов в литературе по квантовой механике известны точные решения. Хорошим примером является потенциал Вудса – Саксона, который описывает уровни энергии нейтрона в ядре атома [3]. Этот потенциал принадлежит к классу I [4]. Потенциалы, входящие в оба класса точно решаемых задач, описывают электромагнитное взаимодействие на атомно – молекулярном уровне и сильное взаимодействие на ядерном и кварковом уровне. С помощью описанного в статье метода могут быть найдены пока ещё неизвестные точные решения и для других потенциалов, входящих в классы I, II.

Библиографическая ссылка