В последние годы в области аддитивной теории чисел произошли большие изменения, например тернарная (слабая) проблема Гольдбаха в 2013 г. была решена, Харальдом Хельготт. Про бинарную (сильную) проблему многие считают, что эта гипотеза недоказуема, будто б наблюдаемая закономерность является сложной комбинацией математических совпадений. Это ассоциируется с тем, что еще не нашли закона распределения простых чисел. Хотя автором получено распределение параметров простых чисел PN и составных чисел CN на базе множества Θ = {6k ± 1/ где параметр k∈N}. (Distribution of parameters of Composite and Prime Numbers – DCPN), [1].
Целью настоящей статьи является решение проблемы Гольдбаха-Эйлера, т.е. доказательство того, что любое четное число ζ > 2 представима в виде суммы двух простых чисел или другими словами предлагается разрешимость Диофантового уравнения ζ = x + y, где ζ – четное число и (x, y)∈P.
В работе рассматриваются свойства четных чисел ζ > 8 сравнимых c m по mod 6 соответственно по остаткам m = 0, 2, 4. Приводятся представления чётных чисел ζ = 6ν + m в виде суммы двух элементов θ1 + θ2 из множества Θ.
Бинарная проблема Гольдбаха-Эйлера выполнима и на множестве близнецов простых чисел Tw, когда параметры 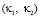 элементов θ1 и θ2 принадлежат к множеству параметров чисел близнецов, т.е.
элементов θ1 и θ2 принадлежат к множеству параметров чисел близнецов, т.е. 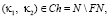 где FN – объединение параметров составных чисел в множестве Θ. Для программного обеспечения проблемы используются свойства четных чисел
где FN – объединение параметров составных чисел в множестве Θ. Для программного обеспечения проблемы используются свойства четных чисел 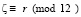 и тождества полученные соответственно по свойствам четных чисел ζ > 8. Приведены примеры разложений чётных чисел ζ > 8 с помощью программ Gold –P и Gold Tw как по всем простым числам P, так и по множеству близнецов простых чисел Tw. На предстваленные алгоритмы даны описания и листинги программ на Software Module ACCESS.
и тождества полученные соответственно по свойствам четных чисел ζ > 8. Приведены примеры разложений чётных чисел ζ > 8 с помощью программ Gold –P и Gold Tw как по всем простым числам P, так и по множеству близнецов простых чисел Tw. На предстваленные алгоритмы даны описания и листинги программ на Software Module ACCESS.
Краткий обзор по проблеме Гольдбаха-Эйлера
В 1922 г. Харди и Литлвуд доказали с помощью своего известного аналитического метода [5], что предположение Гольдбаха верна для всех достаточно больших нечетных чисел, если дзета функция ζ(s) и функция L(s, χ) не имеют нулей при Re s ≥ 3/4. Есть предположение, что методами Харди–Литлвуд и Рамануджана в форме тригонометрических сумм И.М. Виноградова можно получить асимптотические формулы, т.е. доказать «почти все» четные числа представимы суммами двух простых чисел, однако, потребуется бесконечно много исключений [3, 6]. В 1930 Шнирельман показал, что целое число есть сумма не более чем const C = 800 000 простых чисел. Однако, в 1995 г. Оливер Рамаре получил, что четное число есть сумма неболее чем шесть простых чисел. В 1966 Chen Jingrun доказал, что любое достаточно большое чётное число представимо в виде суммы простых чисел или в виде суммы простого числа и полупростого (произведение двух простых чисел). В работах Харди и Литлвуда, Харальд Хельготт заметил, что круговой метод «большие дуги» и «малые дуги» не действуют, влияние малых дуг очень сильные [4] Среди учёных бытует мысль, если бинарная гипотеза Гольдбаха неверна, то найдётся рано или поздно алгоритм , который обнаружит её нарушение.
Бинарная или сильная проблема Гольдбаха-Эйлера
Как приведено в [1] для любого составного числа n∈Θ параметры, которых 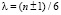 , представимы
, представимы 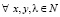 одним из следующих функций:
одним из следующих функций:
1. 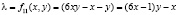
2. 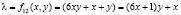
3. 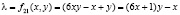
4. 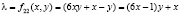 (1)
(1)
Множества значений функций (1) счетные и бесконечные множества, возрастающие по обеим направлениям переменных (x, y), где выражения 1&2 соот ветствуют к составным CN+ и простым числам PN+ вида 6λ + 1, выражения 3&4 соответствуют к составным CN– и простым числам PN– вида 6λ – 1.
Параметры всех составных чисел FN в множестве Θ, счетны как объединение счетных множеств
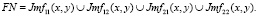
Счетны так же и множества разделенные по подкатегориям соответственно по формам:
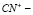 по форме
по форме 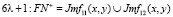
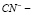 по форме
по форме 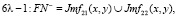 [1].
[1].
Поскольку, простые числа имеют вид 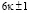 , то сумма элементов
, то сумма элементов 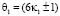 и
и 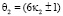 однозначно будут либо
однозначно будут либо
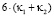 либо
либо 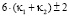 (1’)
(1’)
Очевидно, в обеих случаях θ1 + θ2 являются четными числами. Прежде чем начать доказательство бинарной проблемы Гольдбаха-Эйлера приведём несколько предложений и свойств элементов в множестве Θ.
Предложение 1 Числовые последовательности 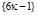 и
и 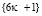 содержат бесконечно много простых чисел
содержат бесконечно много простых чисел
Доказательство. Поскольку, множества FN– и FN+ являются счётными и бесконечными множествами параметров составных чисел в множестве Θ соответственно по формам:  где
где 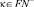 и
и 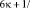 где
где 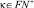 , [1].
, [1].
Стоит поменять, например, для формы 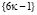 область определения
область определения 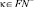 на
на 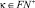 и для формы
и для формы 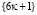 область определения
область определения 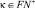 на
на 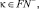 то будут соответственно по формам сгенерированы бесконечно много простых чис ел в силу Предложения 2 из [1], т.к. при таких раскладах параметров не имеют решений Диофантовые уравнения 1&2 и аналогично 3&4 из (1). Если еще и добавить к этим множествам по аналогии форм близнецов простых чисел
то будут соответственно по формам сгенерированы бесконечно много простых чис ел в силу Предложения 2 из [1], т.к. при таких раскладах параметров не имеют решений Диофантовые уравнения 1&2 и аналогично 3&4 из (1). Если еще и добавить к этим множествам по аналогии форм близнецов простых чисел 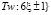 параметры, которых
параметры, которых 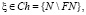 где Сh есть бесконечное множество в силу теоремы о бесконечности близнецов простых чисел Tw, [1]. И учитывая, что объединение бесконечных множеств есть бесконечное мно жество, то числовые последовательности
где Сh есть бесконечное множество в силу теоремы о бесконечности близнецов простых чисел Tw, [1]. И учитывая, что объединение бесконечных множеств есть бесконечное мно жество, то числовые последовательности 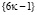 и
и 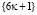 содержат бесконечно много простых чисел, т.е. в точности множества PN– и PN+, [1].
содержат бесконечно много простых чисел, т.е. в точности множества PN– и PN+, [1].
Предложение 2 Любое чётное число 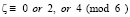
Доказательство. Пусть четное число ζ = 2n, n∈N, тогда 2n/6 = n/3т.е. n принимает форму 3q + α, где q∈N и естественно α = (0, 1, 2).
При 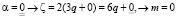 т.е. делится нацело на 6,
т.е. делится нацело на 6,
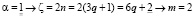
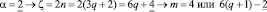
Предложение 3 Любое четное число ζ > 8 есть сумма 2-х элементов Θ
Доказательство. 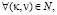 рассмотрим случаи деления четного числа ζ на 6 (шесть) соответственно по остаткам (0, 2 и 4), тогда имеем случаи:
рассмотрим случаи деления четного числа ζ на 6 (шесть) соответственно по остаткам (0, 2 и 4), тогда имеем случаи:
1) 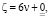 пусть
пусть 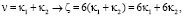 (добавим и отнимем 1 (единицу), тогда имеем:
(добавим и отнимем 1 (единицу), тогда имеем: 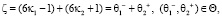
2) 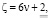 пусть
пусть
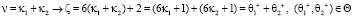
3) 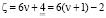 пусть
пусть
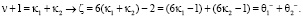
Свойства и представления чётных чисел ζ > 8 в множестве Θ
Пусть 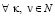 четное число
четное число 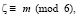 где m = (0, 2, 4) тогда имеем следующие свойства элементов Θ разделенные соответственно по остаткам m:
где m = (0, 2, 4) тогда имеем следующие свойства элементов Θ разделенные соответственно по остаткам m:
α) Если к числам 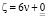 добавить и отнять числа вида
добавить и отнять числа вида 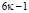 , то будем иметь:
, то будем иметь: 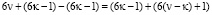 и точно также если добавить и отнять числа
и точно также если добавить и отнять числа 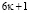 , имеем
, имеем 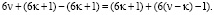
Значит, 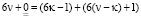 или
или
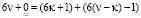 (2)
(2)
выполнимо также и тождество
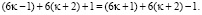 (2’)
(2’)
Пусть 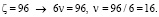 Для θ1=6k+1 и θ2=6(ν-k) при k=1→ θ1= 7, θ2=89. Для θ1=6k-1 и θ2=6(ν-k)+1 при k=1→ θ1=5, θ2=91
Для θ1=6k+1 и θ2=6(ν-k) при k=1→ θ1= 7, θ2=89. Для θ1=6k-1 и θ2=6(ν-k)+1 при k=1→ θ1=5, θ2=91
β) Если к числам 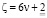 добавить и отнять
добавить и отнять 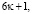 то будем иметь:
то будем иметь:
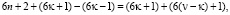 тогда следует, что
тогда следует, что
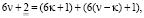 (3)
(3)
выполнимо также и тождество
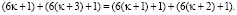 (3’)
(3’)
Пусть 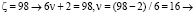 из (3), при k = 1 θ1=7, θ2=91
из (3), при k = 1 θ1=7, θ2=91
γ) Если числам 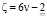 (добавить и отнять числа вида
(добавить и отнять числа вида 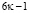 ) будем иметь:
) будем иметь:
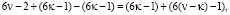 следовательно, имеем
следовательно, имеем
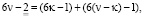 (4)
(4)
выполнимо также и тождество
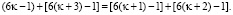 (4’)
(4’)
Пусть 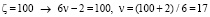 и из (4) при k=1→ θ1=5, θ2=95
и из (4) при k=1→ θ1=5, θ2=95
Теорема (Euler) Любое четное число ζ > 2 представима в виде суммы двух простых чисел
Доказательство разложения четных чисел ζ ≤ 8 на сумму двух простых чисел, очевидны. Рассмотрим разложение для четных чисел ζ > 8. Четные числа ζ согласно свойствам α, β, γпредставимы элементами множества Θ в виде сумм двух чисел: θ1=6ki±1 и θ2=6(ν-ki)±1, где 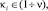
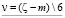 соответственно по остаткам
соответственно по остаткам 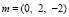 следующим образом:
следующим образом:
а. для 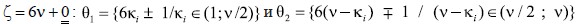
б. для 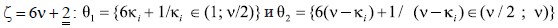 (5)
(5)
в. для 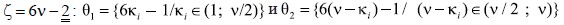
Очевидно из (5) следует, что чётные числа ζ представляются суммами ν/2 пар элементов из множества Θ. Поскольку рассматриваются чётные числа ζ > 8, то значение ν > 1, ибо 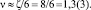 Параметры пробегают интевал (1÷ν) последовательно по натуральному ряду чисел. Т.к. натуральные числа являются параметрами множеств: PPCN – простых и составных чисел; PTw – близнецов простых чисел; PTwCN – близнецов составных чисел и из того, что в любом интервале (1÷ν) число параметров
Параметры пробегают интевал (1÷ν) последовательно по натуральному ряду чисел. Т.к. натуральные числа являются параметрами множеств: PPCN – простых и составных чисел; PTw – близнецов простых чисел; PTwCN – близнецов составных чисел и из того, что в любом интервале (1÷ν) число параметров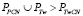 , [2]) тогда следует, что обязательно найдутся в заданном интервале параметры
, [2]) тогда следует, что обязательно найдутся в заданном интервале параметры 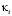 для которых одна из форм
для которых одна из форм 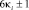 будет простым числом. Значит в проколотом интервале
будет простым числом. Значит в проколотом интервале 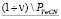 останутся лишь параметры
останутся лишь параметры 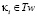 и
и 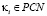 (см. ниже в примерах). При параметрах близнецов простых чисел PTw, оба элемента θ1 и θ2 являются простыми числами. Простыми числами также являются и как уже убедились из Предложения 1 следующие сочетания форм с областями определений:
(см. ниже в примерах). При параметрах близнецов простых чисел PTw, оба элемента θ1 и θ2 являются простыми числами. Простыми числами также являются и как уже убедились из Предложения 1 следующие сочетания форм с областями определений:
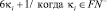 ,
,
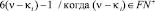 и
и
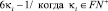 ,
,
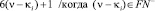 (6)
(6)
Значит проблема Гольдбаха-Эйлера решается однозначно положительно, ибо для любого четного числа 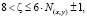 где
где 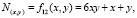 (x, y) = 1, 2, 3… в интервале
(x, y) = 1, 2, 3… в интервале 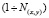 всегда существуют элементы из FN+ и FN–, поскольку при (x, y)∈N значения функций f11(x, y), f21(x, y), f22(x, y), очевидно,
всегда существуют элементы из FN+ и FN–, поскольку при (x, y)∈N значения функций f11(x, y), f21(x, y), f22(x, y), очевидно, 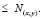 Если одно из выражений:
Если одно из выражений: 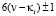 или
или 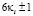 будет составным числом, то при переходе на следующие параметры
будет составным числом, то при переходе на следующие параметры 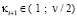 картина изменится в силу закона распределения параметров составных и простых чисел
картина изменится в силу закона распределения параметров составных и простых чисел 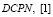 (см. табл. 2). Много примеров подтверждено программой
(см. табл. 2). Много примеров подтверждено программой 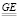 для разложения четных чисел начиная с заданного параметра
для разложения четных чисел начиная с заданного параметра 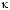 = значению поля [sk].
= значению поля [sk].
Таблица 2
Распределение параметров составных и простых чисел Θ
|
Id |
F1 |
F2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
1 |
+ |
+ |
41 |
- |
- |
81 |
+ |
- |
121 |
+ |
- |
161 |
+ |
- |
|
2 |
+ |
+ |
42 |
- |
+ |
82 |
- |
+ |
122 |
+ |
- |
162 |
- |
+ |
|
3 |
+ |
+ |
43 |
- |
+ |
83 |
+ |
- |
123 |
+ |
- |
163 |
- |
+ |
|
4 |
- |
+ |
44 |
- |
+ |
84 |
- |
+ |
124 |
- |
+ |
164 |
- |
+ |
|
5 |
+ |
+ |
45 |
+ |
+ |
85 |
- |
+ |
125 |
+ |
- |
165 |
+ |
- |
|
6 |
+ |
- |
46 |
+ |
- |
86 |
- |
- |
126 |
+ |
- |
166 |
+ |
- |
|
7 |
+ |
+ |
47 |
+ |
+ |
87 |
+ |
+ |
127 |
- |
+ |
167 |
- |
- |
|
8 |
- |
+ |
48 |
- |
- |
88 |
- |
- |
128 |
+ |
- |
168 |
+ |
- |
|
9 |
- |
+ |
49 |
- |
+ |
89 |
- |
- |
129 |
- |
+ |
169 |
- |
+ |
|
10 |
+ |
+ |
50 |
- |
- |
90 |
+ |
- |
130 |
- |
- |
170 |
+ |
+ |
|
11 |
+ |
- |
51 |
+ |
- |
91 |
+ |
- |
131 |
+ |
- |
171 |
- |
- |
|
12 |
+ |
+ |
52 |
+ |
+ |
92 |
- |
- |
132 |
- |
- |
172 |
+ |
+ |
|
13 |
+ |
- |
53 |
- |
+ |
93 |
- |
+ |
133 |
- |
+ |
173 |
+ |
- |
|
14 |
- |
+ |
54 |
- |
- |
94 |
- |
+ |
134 |
- |
- |
174 |
- |
- |
|
15 |
- |
+ |
55 |
+ |
- |
95 |
+ |
+ |
135 |
+ |
+ |
175 |
+ |
+ |
|
16 |
+ |
- |
56 |
+ |
- |
96 |
+ |
- |
136 |
- |
- |
176 |
- |
- |
|
17 |
+ |
+ |
57 |
- |
- |
97 |
- |
- |
137 |
+ |
+ |
177 |
+ |
+ |
|
18 |
+ |
+ |
58 |
+ |
+ |
98 |
- |
+ |
138 |
+ |
+ |
178 |
+ |
- |
|
19 |
- |
+ |
59 |
- |
+ |
99 |
- |
+ |
139 |
- |
- |
179 |
- |
- |
|
20 |
- |
- |
60 |
- |
+ |
100 |
+ |
+ |
140 |
- |
+ |
180 |
- |
- |
|
21 |
+ |
- |
61 |
+ |
- |
101 |
+ |
- |
141 |
- |
- |
181 |
+ |
- |
|
22 |
- |
+ |
62 |
+ |
- |
102 |
+ |
- |
142 |
+ |
- |
182 |
+ |
+ |
|
23 |
+ |
+ |
63 |
+ |
- |
103 |
+ |
+ |
143 |
+ |
+ |
183 |
- |
+ |
|
24 |
- |
- |
64 |
- |
+ |
104 |
- |
- |
144 |
- |
+ |
184 |
- |
+ |
|
25 |
+ |
+ |
65 |
- |
+ |
105 |
+ |
- |
145 |
- |
- |
185 |
- |
+ |
|
26 |
+ |
- |
66 |
+ |
- |
106 |
- |
- |
146 |
+ |
- |
186 |
+ |
- |
|
27 |
+ |
- |
67 |
- |
+ |
107 |
+ |
+ |
147 |
+ |
+ |
187 |
+ |
- |
|
28 |
- |
+ |
68 |
+ |
- |
108 |
- |
+ |
148 |
- |
+ |
188 |
+ |
- |
|
29 |
- |
+ |
69 |
- |
- |
109 |
- |
+ |
149 |
- |
- |
189 |
- |
- |
|
30 |
+ |
+ |
70 |
+ |
+ |
110 |
+ |
+ |
150 |
- |
- |
190 |
- |
- |
|
31 |
- |
- |
71 |
- |
- |
111 |
- |
- |
151 |
+ |
- |
191 |
- |
- |
|
32 |
+ |
+ |
72 |
+ |
+ |
112 |
+ |
- |
152 |
- |
+ |
192 |
+ |
+ |
|
33 |
+ |
+ |
73 |
+ |
- |
113 |
- |
+ |
153 |
+ |
- |
193 |
- |
- |
|
Окончание табл. 2 |
||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
34 |
- |
- |
74 |
- |
+ |
114 |
- |
+ |
154 |
- |
- |
194 |
- |
+ |
|
35 |
+ |
- |
75 |
- |
+ |
115 |
+ |
- |
155 |
- |
+ |
195 |
+ |
- |
|
36 |
- |
- |
76 |
+ |
- |
116 |
- |
- |
156 |
+ |
- |
196 |
- |
- |
|
37 |
+ |
- |
77 |
+ |
+ |
117 |
- |
+ |
157 |
- |
+ |
197 |
- |
+ |
|
38 |
+ |
+ |
78 |
- |
+ |
118 |
+ |
- |
158 |
- |
+ |
198 |
- |
+ |
|
39 |
- |
+ |
79 |
- |
- |
119 |
- |
- |
159 |
- |
+ |
199 |
- |
+ |
|
40 |
+ |
+ |
80 |
- |
+ |
120 |
- |
+ |
160 |
- |
- |
200 |
+ |
- |
Параметры чисел близнецов Tw от 1 до 6100:
Сh = {1, 2, 3, 5, 7, 10, 12, 17, 18, 23, 25, 30, 32, 33, 38, 40, 45, 47, 52, 58, 70, 72, 77, 87, 95, 100, 103, 107, 110, 135, 137, 138, 143, 147, 170, 172, 175, 177, 182, 192, 205, 213, 215, 217, 220, 238, 242, 247, 248, 268, 270, 278, 283, 287, 298, 312, 313, 322, 325, 333, 338, 347, 348, 352, 355, 357, 373, 378, 385, 390, 397, 425, 432, 443, 448, 452, 455, 465, 467, 495, 500, 520, 528, 542, 543, 550, 555, 560, 562, 565, 577, 578, 588, 590, 593, 597, 612, 628, 637, 642, 653, 655, 667, 670, 675, 682, 688, 693, 703, 705, 707, 710, 712, 723, 737, 747, 753, 758, 773, 775, 787, 798, 800, 822, 828, 835, 837, 850, 872, 880, 903, 907, 913, 917, 920, 940, 942, 943, 957, 975, 978, 980, 1015}
Пример 1. Пусть чётное число 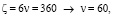 выпишем параметры:
выпишем параметры:
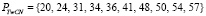 (см. Теорему 1, [2])
(см. Теорему 1, [2])
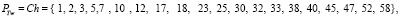
Таблица 1
Формирование параметров составных чисел в множестве Θ
|
f11 = 6xy – x – y |
f12 = 6xy + x + y |
f21 = 6xy – x + y |
f22 = 6xy + x – y |
||
|
x |
y |
||||
|
1 |
1 |
4 |
8 |
6 |
6 |
|
2 |
9 |
15 |
13 |
11 |
|
|
3 |
14 |
22 |
20 |
16 |
|
|
4 |
19 |
29 |
27 |
21 |
|
|
5 |
24 |
36 |
34 |
26 |
|
|
6 |
29 |
43 |
41 |
31 |
|
|
7 |
34 |
50 |
48 |
36 |
|
|
8 9 10 |
39 44 49 |
57 64 71 |
55 62 69 |
41 46 51 |
|
|
2 |
2 |
20 |
28 |
24 |
24 |
|
3 |
31 |
41 |
37 |
35 |
|
|
4 |
42 |
54 |
50 |
46 |
|
|
5 |
53 |
67 |
63 |
57 |
|
|
6 |
64 |
80 |
76 |
68 |
|
|
7 |
75 |
93 |
89 |
79 |
|
|
8 9 10 |
86 97 108 |
106 119 132 |
102 115 128 |
90 101 112 |
|
|
3 |
3 |
48 |
60 |
54 |
54 |
|
4 |
65 |
79 |
73 |
71 |
|
|
5 |
82 |
98 |
92 |
88 |
|
|
6 |
99 |
117 |
111 |
105 |
|
|
7 |
116 |
136 |
130 |
122 |
|
|
8 9 10 |
133 150 167 |
155 174 193 |
149 168 187 |
139 156 173 |
|
|
4 |
4 |
88 |
104 |
96 |
96 |
|
5 |
111 |
129 |
121 |
119 |
|
|
6 |
134 |
154 |
146 |
142 |
|
|
7 |
157 |
179 |
171 |
165 |
|
|
8 9 10 |
180 203 226 |
204 229 254 |
196 221 246 |
188 211 234 |
|
|
5 |
5 |
140 |
160 |
150 |
150 |
|
6 |
169 |
191 |
181 |
179 |
|
|
7 |
198 |
222 |
212 |
208 |
|
|
8 9 10 |
227 256 285 |
253 284 315 |
243 274 305 |
237 266 295 |
|
|
6 |
6 |
204 |
228 |
216 |
216 |
|
7 |
239 |
265 |
253 |
251 |
|
|
8 9 10 |
274 309 344 |
302 339 376 |
290 327 364 |
286 321 356 |
|
|
7 |
7 |
280 |
308 |
294 |
294 |
|
8 9 10 |
321 362 403 |
351 394 437 |
337 380 423 |
335 376 417 |
|
|
8 |
8 9 10 |
368 415 462 |
400 449 498 |
384 433 482 |
384 431 478 |
|
9 10 |
9 10 10 |
468 521 580 |
504 559 620 |
486 541 600 |
486 539 600 |
Для элементов множеств FN– и FN+ (см. табл. 1), из-за малой размерности табл. 1 могут и отсутствовать некоторые параметры), в данном случае имеем:
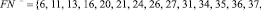
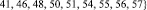
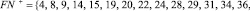
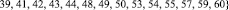
Рассмотрим элементы 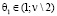 и
и 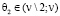 по аналогии с (5.а) в проколотом интервале
по аналогии с (5.а) в проколотом интервале 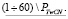
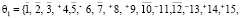
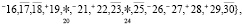
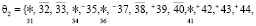
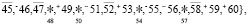
Пусть по элементам θ1 рассматриваются только параметры близнецов простых чисел 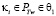 тогда легко замеметить, что уже не играет роли к какому типу множеств FN– или FN+ относятся соответствующие параметры из θ2. Тоже самое верно и для θ2 если
тогда легко замеметить, что уже не играет роли к какому типу множеств FN– или FN+ относятся соответствующие параметры из θ2. Тоже самое верно и для θ2 если 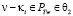 , не играет роли к какому типу множеств FN– или FN+ относятся соответствующие параметры θ1, ибо при любом варианте для форм
, не играет роли к какому типу множеств FN– или FN+ относятся соответствующие параметры θ1, ибо при любом варианте для форм 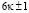 когда параметр
когда параметр 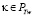 являются простыми числами близнецов, простыми также будут числа соответствующие условиям (6), один из форм будет простым числом, в силу Предложения 1, напр.,
являются простыми числами близнецов, простыми также будут числа соответствующие условиям (6), один из форм будет простым числом, в силу Предложения 1, напр.,
1. 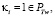 тогда параметр θ2:
тогда параметр θ2:
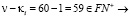 имеем два случая
имеем два случая
γ. 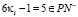 ,
,
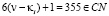
δ. 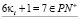 ,
,
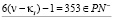
2. 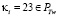
тогда 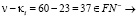 имеем два случая
имеем два случая
γ. 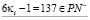 ,
,
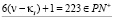
δ. 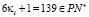 ,
,
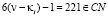 , и т.д.
, и т.д.
Значит 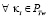 в любом одном из 2-х вариантов (γ, δ) всегда имеется сумма простых чисел. Рассмотрим варианты когда параметры принадлежат к множествам FN– или FN+, например
в любом одном из 2-х вариантов (γ, δ) всегда имеется сумма простых чисел. Рассмотрим варианты когда параметры принадлежат к множествам FN– или FN+, например
3. 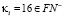 , тогда
, тогда
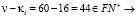
γ. 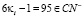 ,
,
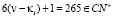
δ. 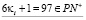 ,
,
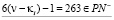
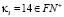 тогда
тогда
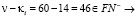
γ. 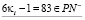 ,
,
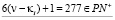
δ. 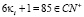 ,
,
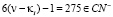
Пример 2. Чётное число ζ = 6ν + 2 = 362, найдём ν = 60. Параметры PTwCN, PTw, FN–, FN+, такие же как и в Примере 1. Рассмотрим в соответствии с (5.б) в проколотом интервале (1÷60)\PTwCN. Элементы θ1 и θ2 такие же как и в Примере 1.
Для того, чтобы элементы θ1 и θ2 были простыми числами, очевидно из (6) следует, что параметры 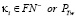 и
и 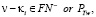 например:
например:
1. 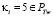 и
и
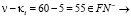
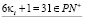 ,
,
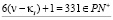
2. 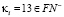 и
и
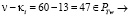
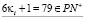 ,
,
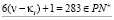
3. 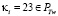 и
и 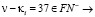
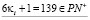 ,
,
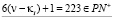
Пример 3. Чётное число ζ = 6ν – 2 = 364, найдём ν = 61. Параметры PTwCN, PTw, FN–, FN+, θ1 и θ2 такие же как и в Примере 1. Рассмотрим в соответствии с (5.в) в проколотом интервале (1÷60)\PTwCN. Для того, чтобы элементы θ1 и θ2 были простыми числами, очевидно из (6) следует, что параметры 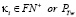 и
и 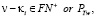 например:
например:
1. 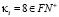 и
и 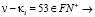
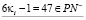 ,
, 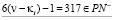
2. 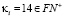 и
и 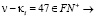
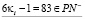 ,
, 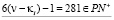
Описание программы Gold-P
Вначале в поле П2 проверяется число на четность и какому типу четных чисел оно относится. Согласно свойств четных чисел 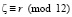 (см. ниже) формируется программой элемент р1∈Θ соответствующий к типу числа.
(см. ниже) формируется программой элемент р1∈Θ соответствующий к типу числа.
После тестирования чисел р1 и П2 – р1 на простоту делается анализ если числа простые, то всё нормально, иначе переход на следующий k1 = k1 + 1 шаг.
Private Sub Gold-P Click() Algorithm Goldbach – Euler for pairs of
Dim k1,k2,m1,m2 As String primes of an even number
If sl4<10 or Not (Right(Π2,1) Mod 2 = 0 Then
Π4 = “ It is sl4<10 or cannot be <not even number>”
Else
Ora1=Time(), ora2=””
k1=sk, Π4 =sl4, Π4 =Ost(sl4,12,ss)
s1: If Π4 =0 or Π4 =4 or Π4 =6 or Π4 =10 Then p1=6*k1-1
If Π4 =2 or Π4 =8 Then p1=6*k1+1
m1=PFA(p1,ss)
If m1 =”+” Then
k1=k1+1
GoTo s1
Else
End If
p2=vich(Π2,p1,ss), m2= PFA(p2,ss)
If m2 =”-” Then
If p1+p2=0+Π2 Then
πχ1=p1, πχ2=p2, ora2= Time()
sk=k1, Π2=sl1
Else
k1=k1+1
GoTo s1
End If
Else
k1=k1+1
GoTo s1
End If
End If
Π2=sl1, sl1 =”” End Sub
Описание программы Gold-Tw
Вначале в поле П2 проверяется число на четность и какому типу четных чисел оно относится. Согласно свойств четных чисел 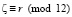 (см. ниже) формируется программой элемент р1∈Θ соответствующий к типу числа и в зависимости от значения поля [sk], т.е. c какого номера начать соответствующий элемент р1∈Θ. После тестирования числа р1 на простоту делается еще и анализ на то, что является ли число простым и есть ли число р1∈Tw. И точно также проверяется число (П2 – р1)∈Tw если «да», то всё нормально, иначе переход на следующий шаг k1 = k1 + 1 к поиску нового р1∈Tw и т.д.
(см. ниже) формируется программой элемент р1∈Θ соответствующий к типу числа и в зависимости от значения поля [sk], т.е. c какого номера начать соответствующий элемент р1∈Θ. После тестирования числа р1 на простоту делается еще и анализ на то, что является ли число простым и есть ли число р1∈Tw. И точно также проверяется число (П2 – р1)∈Tw если «да», то всё нормально, иначе переход на следующий шаг k1 = k1 + 1 к поиску нового р1∈Tw и т.д.
Private Sub Gold-Tw Click() Algorithm Goldbach – Euler for pairs of
Dim k1,k2,m1,m2 As String twin’s of an even number
sl1=Π2, Π2=sl4
If 0+ Π2 ≤ 0+sk Then sk=1
If sl4 ≤ 10 or Not (Right(Π2,1) Mod 2= 0 Then
Π4= ”It is sl4<10 or cannot be < not even numbers >”
Else
Ora1=Time(), Ora2=”” , k1=sk, Π4= sl4, Π4= Ost(sl4, 12, ss)
s1: If Π4= 0 or Π4= 4 or Π4= 6 or Π4= 10 Then p1=6*k1-1
If Π4= 2 or Π4= 8 Then p1=6*k1+1
m1=PFA(p1, ss)
If m1=”+” Then
k1=k1+1
GoTo s1
Else
m1=PFA(slg(p1, 2, ss), ss), m2=PFA(vich(p1, 2, ss), ss)
If m1=”+” And m2=”+” Then GoTo s2
End if
Π5=dln(Π2, 6, ss), πχ3=k1, p2= vich(Π2, p1, ss), m2= PFA(p2, ss)
If m2=”-“ Then
If p1+p2=0+ Π2 Then
πχ1=p1, πχ2=p2, πχ4=dln(p2, 6, ss)
sk=k1, Π2=sl1, Ora2= Time()
m2=PFA(slg(p2,2,ss), ss)
m3=PFA(vich(p2,2,ss), ss)
If m2=”+” And m3=”+” Then GoTo s2
Else // Подпрограммы
s2: k1=k1+1 1. Ost(sl4, sl1,ss) – остаток от деления больших чисел sl4 на sl1
GoTo s1 2. PFA(p1,ss) – проверяет число p1 на простоту
End if 3. vich(sl4,p1,ss) – вычитание больших чисел sl4 и sl1
Else 4. slg(sl4, sl1, ss) – сложение больших чисел sl4 и sl1
k1=k1+1 5. dln(sl4, sl1, ss) – деление больших чисел sl4 и sl1
GoTo s1
End if, Π2=sl1, sl1=”” End Sub
Представление чётных чисел
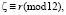 где
где 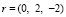
1. Чётные числа вида: ζ = 12τ. Количество пар (р1, р2) чисел в сумме дающих ζ равно 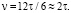 Очевидно из (5) следует, что эти пары чисел в Θ, имеют вид:
Очевидно из (5) следует, что эти пары чисел в Θ, имеют вид: 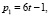
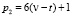 и
и 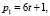
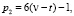 где t и ν – t принадлежат к множеству PTw, [], т.е. (р1 и р2) числа – Tw.
где t и ν – t принадлежат к множеству PTw, [], т.е. (р1 и р2) числа – Tw.
2. Чётные числа: 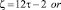
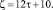 Количество пар (р1, р2) в сумме дающих ζ равно
Количество пар (р1, р2) в сумме дающих ζ равно 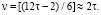 Очевидно из (5) следует, что эти пары чисел в Θ имеют следующий вид:
Очевидно из (5) следует, что эти пары чисел в Θ имеют следующий вид: 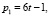 и
и 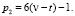
3. Чётные числа вида: 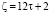 количество пар чисел (р1, р2) в сумме дающих ζ равно
количество пар чисел (р1, р2) в сумме дающих ζ равно 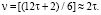 Очевидно из (5) следует, что эти пары чисел в Θ имеют следующий вид:
Очевидно из (5) следует, что эти пары чисел в Θ имеют следующий вид: 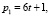 и
и 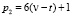 .
.
4. Чётные числа вида: 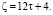 Количество пар чисел (р1, р2) в сумме дающих ζ равно
Количество пар чисел (р1, р2) в сумме дающих ζ равно 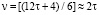 имеют вид:
имеют вид: 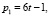
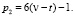
5. Чётные числа вида: 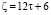 . Количество пар чисел (р1, р2) в сумме дающих ζ равно
. Количество пар чисел (р1, р2) в сумме дающих ζ равно 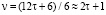 имеют вид:
имеют вид: 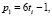
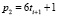 or
or 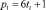 и
и 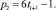
6. Чётные числа вида: 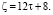 Количество пар чисел (р1, р2) в сумме дающих ζ равно
Количество пар чисел (р1, р2) в сумме дающих ζ равно 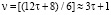 имеют вид:
имеют вид: 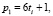
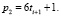
Примеры полученные прогаммой Gold-P и Gold-Tw:

. . . .
Заключение
В работе дано доказательство бесконечности простых чисел в числовых последовательностях 6n – 1 и 6n + 1. Приведены свойства чётных чисел ζ > 8 и их представления в виде форм 6n + m, где m = (0, 2, 4) с суммами двух элементов 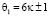 и
и 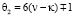 из множества Θ.
из множества Θ.
Дано доказательство о представлении четного числа ζ > 2 на сумму двух простых чисел.
Библиографическая ссылка
Чермидов С.И. БИНАРНАЯ ПРОБЛЕМА ГОЛЬДБАХА-ЭЙЛЕРА В МНОЖЕСТВЕ Θ = {6K ±1/K∈N} // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 5-2. – С. 207-215;URL: https://applied-research.ru/ru/article/view?id=9223 (дата обращения: 23.04.2024).













