Рассматривается мягкая посадка отработавшей первой ступени космического аппарата (КА). (Мягкая посадка в идеале – приземление с нулевой скоростью, в реальности мягкой посадкой считается для пассажирского самолета касание земли при вертикальной скорости снижения не превышающей 2 м/с, для КА – не превышающей 6 м/с.) Такие зарубежные фирмы, как Space Exploration Technologies Corporation (SpaceX) и Blue Origin, реализовали проекты, осуществляющие мягкую посадку первых ступеней, и даже использовали их вторично при последующих запусках [1, 2].
Оптимальное управление (ОУ) на последнем вертикальном участке приземления по принципу максимума Понтрягина представляет собой вертикальное свободное падение вначале и затем торможение при максимально допустимом (с точки зрения прочности конструкции) значении тяги двигателей. В [3] были проведены расчеты для первой ступени, аналогичной первой ступени Falcon9, позволившие получить оптимальное программное управление при принятом условии одного работающего двигателя ЖРД из силовой установки первой ступени. Математическая модель посадки с ОУ (при использовании принципа максимума Понтрягина) представляет собой краевую задачу для системы обыкновенных дифференциальных уравнений (ОДУ), которая была решена методом пристрелки. Метод пристрелки дает наиболее точные результаты при численном решении краевых задач [4]. К сожалению, существуют определенные трудности в реализации метода пристрелки, в силу чего метод редко используют при решении инженерных задач. Но при определенном опыте работы с методом Ньютона вполне возможно его реализовать даже для задач ОУ с переключением [4, 5].
Особенность реализации подобного управления состоит в том, что конечное значение скорости в момент приземления очень сильно зависит от возможных случайных отклонений от расчетных значений таких параметров, как плотность атмосферного воздуха, коэффициент аэродинамического сопротивления, удельная тяга двигателя, скорость и масса ступени в начальный момент (задается значением начальной высоты вертикального участка приземления). Возможность реализации мягкой посадки с ОУ без обратной связи при возможном случайном отклонении указанных выше параметров (случайные величины (СВ) предполагаются независимыми и подчиняются нормальному закону с небольшими отклонениями от расчетных значений, принятых в [3]) рассмотрена в [6]. Вероятность осуществления мягкой посадки с программным ОУ без обратной связи чрезвычайно мала. Алгоритм обратной связи при мягком прилунении предложен в [7]. Проблема мягкой посадки КА рассматривается и в таких работах, как [8–11].
Постановка задачи и математическое моделирование процесса посадки и алгоритма обратной связи
Разработка синтеза ОУ (получения закона поправки на управление при отклонении СВ – алгоритма обратной связи) является темой настоящей работы. В [7] А.М. Летовым была предложена идея использования поправки на тягу основного двигателя в качестве компенсации возможных случайных отклонений при мягком прилунении. Система уравнений движения линеаризовалась и приобретала форму уравнений возмущенного движения. Алгоритм получения обратной связи предлагался следующий:
При функционале вида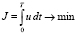 
исходная система состояния:
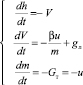, (1)
где h – расстояние от космического аппарата до поверхности Луны, V – скорость космического аппарата (ось скорости направлена вниз), m – масса космического аппарата, Gт = u – расход топлива (управление), Т – конечный момент времени, gл = 1,62 – ускорение свободного падения на Луне, β·u = P – тяга двигателя, коэффициент β пропорционален скорости истечения газа из сопла двигателя (импульс ракетного двигателя).
Система возмущенного движения принимает вид
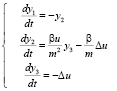, (2)
где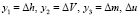 
– поправка на управление.
Функционал выбирался вида
,
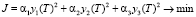где α1, α2, α3 > 0 – весовые коэффициенты. Предлагалось решать системы (1) и (2) последовательно. При этом начальные значения возмущений не предполагались слишком большими и должны были удовлетворять условию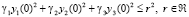 
, γ1, γ2, γ3 – весовые коэффициенты.
Несколько модифицированный по отношению к вышеуказанному алгоритм был применен к задаче мягкого приземления. Исходная система уравнений движения:
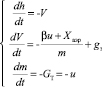. (3)
Система уравнений возмущенного движения:
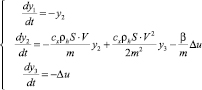, (4)
где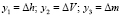 
– возмущения независимых переменных, связанных со случайными факторами, 
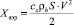– сила аэродинамического сопротивления, cx – коэффициент аэродинамического сопротивления первой ступени ракеты, ρh – плотность воздуха на текущей высоте, S – площадь миделя первой ступени.
Предполагая, что масса ракеты в начале последнего вертикального участка изменяется незначительно, и учитывая малость коэффициента при y3 во втором уравнении, оставим только первые два ДУ в системе возмущенного движения и будем считать, что масса приближенно остается постоянной. Обозначим коэффициенты в системе уравнений возмущенного движения: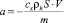 
, 
.
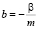Применим к задаче отыскания обратной связи метод аналитического конструирования оптимального регулятора. Хотя применение данного подхода к динамическому процессу, протекающему достаточно малое время, не совсем корректно, попробуем реализовать алгоритм.
Задачу синтеза оптимального регулятора сформулируем следующим образом: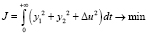 
при линеаризованной и упрощенной системе возмущенного движения:
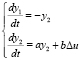(5)
при у1(0) = y10; у2(0) = y20, которые представляют собой отклонения параметров, замеряемых в процессе приземления, от расчетных значений оптимального процесса, полученных при решении системы (3) невозмущенного движения.
Матричное уравнение для отыскания синтезирующей функции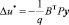 
, полученное из уравнения Беллмана, имеет вид 
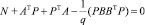. Постановка задачи в общем виде: 
, 
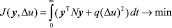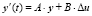. В нашем случае 
.
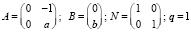Отсюда имеем матричное алгебраическое уравнение с постоянными коэффициентами: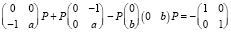 
, где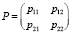 
– симметрическая положительно определенная матрица.
Расписав матричное уравнение покоординатно, получим систему алгебраических уравнений относительно неизвестных элементов матрицы Р.
.
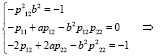
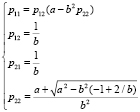Подставляя численные значения коэффициентов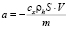 
, 
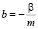в каждый момент измерения скорости и высоты, получим синтезирующую функцию:
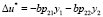. (6)
Алгоритм вычислений имеет следующий вид.
Имеем зависимости h*(t), V*(t), u*(t) – в оптимальном процессе без обратной связи, полученные в [3]. Предположим, что в реальном процессе рассматриваемые СВ (плотность атмосферного воздуха, коэффициент аэродинамического сопротивления, удельная тяга двигателя, скорость и масса ступени в начальный момент) отклоняются от расчетных значений. Тогда при достижении высоты включения двигателя из [3] происходит включение двигателя в реальном процессе. Если при заданной высоте скорость превышает оптимальное значение скорости включения двигателя, то принимаем за высоту включения значение hвкл +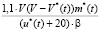 
, где второе слагаемое есть поправка на высоту, полученная из приближенного равенства импульса силы тяги разности импульса скорости в реальном движении и оптимальном. Δhвкл = 
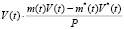, где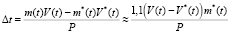 
. При этом предполагается, что двигатель может дросселироваться до 60 %, допустимый расход топлива лежит в диапазоне 195…325 кг/с. Зададимся временем такта измерения высоты и скорости приземления равным 0,04 с (в расчетах это время будет равно шагу интегрирования численного метода решения ОДУ). На каждом шаге интегрирования системы (3) вычисляем отклонения реальных параметров от оптимальных, а также поправку на расход топлива: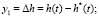 
.
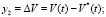
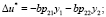
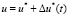В момент времени, когда высота или скорость падения равна нулю, происходит отключение двигателя. Если нулевое значение скорости достигается при h > 0, то с этой высоты происходит свободное падение. Методом Монте-Карло проведем многократные вычисления снижения отработавшей ступени, обработаем статистически полученные данные и в результате сможем оценить вероятность мягкой посадки при выбранных законах распределения СВ.
Результаты расчетов
Для расчетов приземления спускаемого аппарата были взяты исходные данные, полученные в [3].
Свободное падение рассчитывалось с высоты 2000 м. Скорость в оптимальном процессе на этой высоте равна 160 м/с.
Значения переменных, соответствующие моменту включения двигателя в оптимальном процессе:
hвкл = 488,0558 м; Vвкл = 183,82 
; u = Gт = 305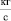 
; m = 20 т; β = 2766 
; сх = 0,8.
Принималось для метода Монте-Карло, моделирующего случайные отклонения расчетных параметров, что отклонения по массе, скорости, сх и плотности воздуха не превышают 5 %, а по удельному импульсу двигателя 1 %. СВ распределены по нормальному закону и независимы. Указанные интервалы составляют диапазон –4σ...+ 4σ. Количество расчетных экспериментов в методе Монте-Карло – 1000.
В качестве зависимости плотности воздуха от высоты в стандартных условиях была принята следующая аппроксимация, дающая удовлетворительную точность до высоты в 20 км:
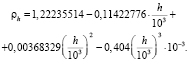
На рис. 1 представлена фазовая траектория в оптимальном процессе.
На рис. 2 представлены полигоны распределения СВ скорости приземления, построенные по средним значениям интервалов распределения, число которых выбиралось равным 20. Указанные кривые соответствуют статистической плотности вероятности.
На рис. 3 – кривые статистической функции вероятности для СВ скорости приземления.
В таблице представлены характеристики полученных распределений скорости приземления для всех трех расчетных случаев.
На рис. 4 и 5 представлено поведение управления и скорости снижения в зависимости от времени для варианта расчета 2 с максимальными отклонениями значений случайных величин. Варианты А и В – маловероятные случаи, характеризующие наихудшие сочетания из выбранных диапазонов изменения СВ.
Вариант А – отклонение по массе и скорости в начальный момент – 5 %, по плотности и сх +5 %, по удельному импульсу двигателя +1 % (Vк = 21,5 м/с).
Вариант В – отклонение по массе и скорости в начальный момент +5 %, по плотности и сх -5 %, по удельному импульсу двигателя -1 % (Vк = 35,7 м/с).
Вариант С – расчетный вариант оптимального управления без отклонений параметров (Vк = 0 м/с).
Заключение
Анализ результатов расчета показал, что данный подход не обеспечивает достаточно высоких значений вероятности обеспечения мягкой посадки. Упрощение уравнений возмущенного движения некорректно, если принять во внимание возможность отклонения массы возвращаемой ступени. Расчет при детерминированном значении массы также не показал удовлетворительного результата (смотри кривые для случая 3 на рис. 2 и 3).
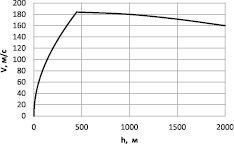
Рис. 1. Зависимость V* = f(h*) в оптимальном процессе
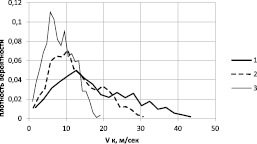
Рис. 2. Полигоны плотности вероятности СВ скорости приземления: 1 – расчет без поправки на управление, 2 – с поправкой на управление по формуле (6), 3 – с поправкой на управление по формуле (6) с отсутствием разброса по массе ступени в начальный момент
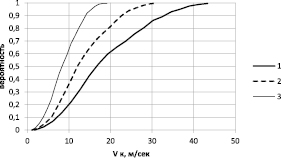
Рис. 3. Статистическая функция распределения для СВ скорости приземления: 1 – расчет без поправки на управление, 2 – с поправкой на управление по формуле (6), 3 – с поправкой на управление по формуле (6) с отсутствием разброса по массе ступени в начальный момент
Параметры распределения скорости приземления для трех рассмотренных случаев
|
Параметры распределения скорости приземления |
M[Vk] Математическое ожидание |
σ[Vk] Среднеквадратическое отклонение |
As[Vk] Коэффициент асимметрии |
Ex[Vk] Коэффициент островершинности |
|
1 |
17,4698 |
9,608866 |
0,551565 |
-0,52408 |
|
2 |
12,51425 |
6,494954 |
0,524414 |
-0,45485 |
|
3 |
8,214698 |
3,841363 |
0,269438 |
-0,67231 |
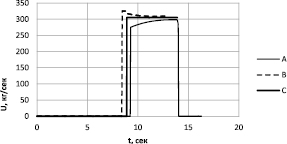
Рис. 4. Управление по времени снижения с высоты 2000 м
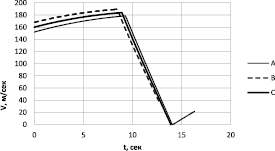
Рис. 5. Изменение скорости по времени снижения
Усложнение системы возмущенного движения и восстановление возможности учета отклонения по массе приведет либо к необходимости аналитического решения системы нелинейных алгебраических уравнений из шести уравнений для отыскания составляющих искомой матрицы Р, либо к попытке численного решения этой системы, обеспечивая при этом нахождение единственного решения для положительной определенности указанной матрицы. Изменение функционала с интегрального типа на терминальный потребует решения системы ДУ Рикатти. В любом случае продолжение работы в указанных направлениях сильно увеличивает трудоемкость численного эксперимента. При этом результаты расчета для детерминированного значения массы не позволяют надеяться на получение удовлетворительного результата и в случае проведения указанной работы. Малое время работы двигателя (порядка 4 с) не позволяет воспользоваться преимуществами теории синтеза оптимального регулятора.
Кроме этого, реализация алгоритма, аналогичного предложенному Летовым в [7], показала его существенный недостаток, а именно невозможность вычисления поправки на тягу при увеличенном времени работы двигателя.