Современный этап научного мировоззрения характерен синергетическим эффектом развития, достигаемым за счет проникновения методологий исследований, характерных для определенных отраслей научных знаний в смежные. Такой подход к познанию экосферы приводит к взаимному и одновременному обогащению используемых классических основ отдельных научных направлений, что может являться гарантом уменьшения или оптимизации воздействия техносферных изменений, инициируемых человеческой деятельностью, на общую среду обитания.
Популяционная динамика – один из разделов математического моделирования, который благодаря универсальности своего подхода и используемого математического аппарата широко используется при решении практически и социально значимых задач математической экологии, демографии и экономики. Основная цель исследований динамики популяций состоит в анализе и прогнозировании численности и плотности взаимодействующих популяций на определенном ареале.
Настоящее исследование посвящено комплексному анализу проблем поведения взаимодействующих популяций с позиций математического и имитационного моделирования.
Материалы и методы исследования
Проведем краткий качественный анализ классической модели «хищник-жертва» [1].
Рассматривается закрытый ареал, в котором обитают жертвы x и хищники y. Взаимодействие популяций описываются системой двух обыкновенных нелинейных дифференциальных уравнений:
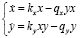, (1)
где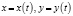 
– функции изменения плотностей особей жертв и хищников во времени t; 
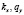– мальтузианские параметры; 
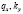– коэффициенты межвидового взаимодействия.
Правые части системы (1) обращаются в ноль в точке
.
В малой окрестности этой точки пр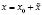и 
и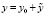 
получим:
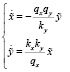(2)
Таким образом, точка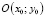 
является невырожденной особой точкой типа «центр», все фазовые траектории системы образуют циклы, а общий интеграл находится так:
.
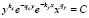В соответствии с системой (2) колебания плотности популяций будут осуществляться по закону
.
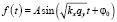На базе модели (1) построим систему с учетом естественной ограниченности плотности популяции жертв:
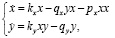(3)
где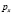 
– параметр внутривидовой конкуренции жертв.
В системе уравнений (3) есть невырожденная особая точка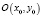 
с координатами:
.
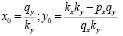Классифицируем особую точку и определим характер поведения системы при малом отклонении от этой точки, для этого сделаем подстановку
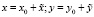
и получим:
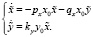
Для данной системы составим характеристическое уравнение:
.
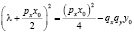При выполнении условия
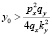
собственные числа будут комплексно-сопряженными с отрицательной действительной частью:
.
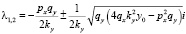Таким образом, точка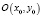 
является «устойчивым фокусом», а фазовые траектории – «логарифмическими спиралями»
Дополним модель (3) логистической функцией для хищника:
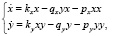
где py – параметр внутривидовой конкуренции хищников.
В данном случае невырожденной особой точкой является точка с координатами:
.
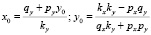Составим систему дифференциальных уравнений для выявления характера поведения системы вблизи найденной особой точки:
.
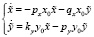Характеристическое уравнение
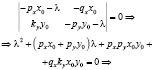
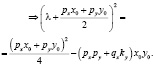
Из характеристического уравнения видно, что действительная часть собственных чисел отрицательная.
Можно показать, что
.
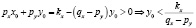Тогда характеристическое уравнение может быть записано следующим образом:
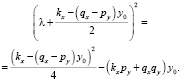
Исходя из полученных соотношений можно получить оценку y0 снизу при которой корни характеристического уравнения будут комплексно-сопряженными:
.
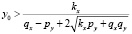При выполнении такого условия корни характеристического уравнения определятся следующим образом:
.
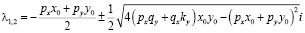Значит, особая точка является «устойчивым фокусом», а фазовые траектории – «логарифмическими спиралями»
Исследуем модель взаимодействия популяций с трофическими функциями:
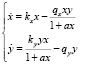или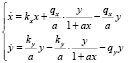 
,
где a – параметр насыщения; ky, qx – коэффициент изменения численности популяций от давления хищника.
Координаты невырожденной особой точки системы будут следующими:
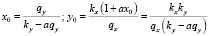. (4)
Исследуем устойчивость системы в особой точке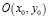 
для чего перейдем к переменным
.
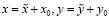Разложим функцию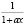 
в ряд Тейлора в окрестности точки x0 сохраняя линейные члены:
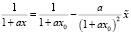. (5)
Тогда система дифференциальных уравнений для определения собственных чисел будет иметь вид:
.
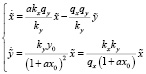Составим характеристическое уравнение системы:
.
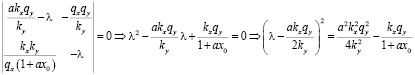Очевидно, действительная часть собственных чисел положительна.
Из (4) следует, что
,
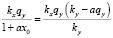тогда можно записать условие, при котором правая часть характеристического уравнения отрицательна:
.
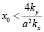В этом случае. собственные числа являются комплексно-сопряженными с положительной действительной частью:
.
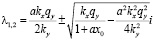Значит, особая точка является неустойчивым фокусом, фазовые траектории – логарифмические спирали
Рассмотрим неклассическую модель типа «хищник-жертва» с трофическими функциями и с функцией насыщения популяции жертв:
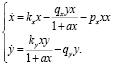(6)
Можно показать, что координаты невырожденной особой точки будут следующими:
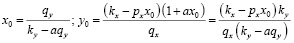
Следствия: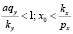 
.
Используя формулу (5) исследуем устойчивость системы в особой точке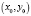 
. Получим следующую систему дифференцированных уравнений:
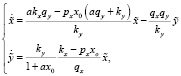
характеристическое уравнение для которой:
.
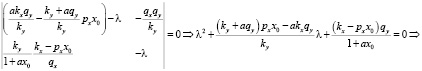
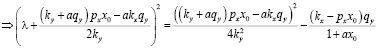Условие, при котором действительная часть характеристического уравнения отрицательна:
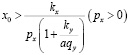. (7)
С учетом величин практических исходных данных выполнение условия (7) гарантирует, что особая точка является устойчивым фокусом, а фазовые траектории – логарифмическими спиралями.
Результаты исследования и их обсуждение
Проведем исследование обобщенной неклассической модели типа «хищник-жертва» с трофическими функциями и с функцией насыщения популяции жертв (6) в среде пакета имитационного моделирования AnyLogic, который поддерживает все известные в настоящее время парадигмы моделирования [2]. Исследование частных моделей взаимодействия популяций проведено, например, в работах [3, 4].
На рис. 1 представлена принципиальная схема модели в среде AnyLogic.
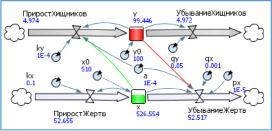
Рис. 1. Схема модели
При выбранных исходных данных
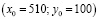
особая точка с координатами
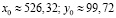
является устойчивым фокусом (см. рис. 2 слева). Фазовые траектории – спирали, закручивающиеся против часовой стрелки от исходной точки внутрь к фокусу.
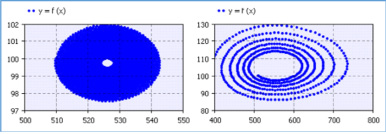
Рис. 2. Фазовые портреты системы с устойчивым и неустойчивым фокусом
Если условие (7) нарушено, то фокус становится неустойчивым (см рис. 2 справа). В этом случае фазовые траектории представляют собой спирали, раскручивающиеся против часовой стрелки от исходной точки, плотность популяций возрастает.
Выводы
Проведенное качественное и количественное исследование задач практической динамики популяций позволило связать воедино классический математический аппарат аналитических исследований и возможности современных идеологий имитационного моделирования, основанные на парадигме системно-динамического анализа.
Представленные в работе математические модели, формальные зависимости и оценки устойчивости получаемых решений апробированы и подтверждены в результате имитационных экспериментов, выполненных на базе аналитической платформы AnyLogic.
Предложенная методология научного исследования является унифицированной и позволяет строить стратегические модели необходимые для принятия управленческих решений с целью минимизации возможных негативных воздействий на экосферу и решать комплексные вопросы оценки характера взаимодействия конкурирующих сообществ и сложных социально-экономических объектов.