Рассмотрим дифференциальный оператор третьего порядка, задаваемый дифференциальным уравнением:
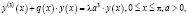(1)
с разделёнными граничными условиями самого общего вида:
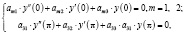(2)
где λ – спектральный параметр,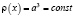 
– весовая функция, потенциал 
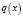– суммируемая функция:
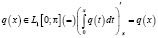почти всюду на 
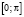. (3)
Пусть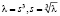 
– фиксированная ветвь корня, причём 
.
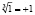Пусть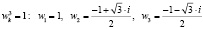 
.
В работе [1] нами доказана следующая теорема.
Теорема 1. Общее решение дифференциального уравнения (1) имеет вид:
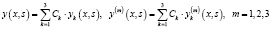, (4)
где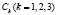 
– произвольные постоянные, причём при 
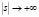имеем:
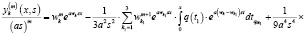
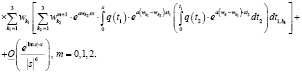(5)
Изучение граничных условий (2) зависит от коэффициентов и проводится с использованием методики работ [2] и [3]. Например, если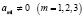 
, то граничные условия (2) можно упростить до равносильных условий вида
.
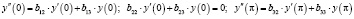В качестве примера таких разделённых граничных условий рассмотрим следующие:
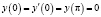. (6)
По терминологии Наймарка М.А. [4, с. 66-77] граничные условия (6) являются нерегулярными. Ранее асимптотика собственных значений краевых задач с нерегулярными граничными условиями (даже в случае гладкого потенциала) фактически не изучалась.
Теорема 2. Асимптотика собственных значений дифференциального оператора (1)-(2) с граничными условиями (6) имеет следующий вид:
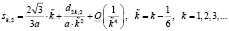, (7)
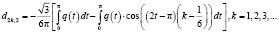(8)