Пусть 
– взаимно простые натуральные числа, 
– наборы случайных величин, распределенных равномерно на множестве вычетов по модулю М. Рассмотрим последовательность, построенную по правилу
(1)
где 
Ее принято называть случайной мультициклической последовательностью. Величину 
принято называть полным циклом мультициклической последовательности .
Если наборы 
независимы, а случайные величины 
образующие j-й набор, независимы и распределены равномерно на множестве вычетов по модулю М последовательность вида представляет собой математическую модель выходной последовательности генератора Пола (см. [6]), в которой наборы 
представляют собой заполнения регистров длин 
. Эта модель используется для изучения статистических свойств выходной последовательности этого генератора.
В работе [1] был исследован случай мультициклической последовательности по модулю 2 с независимыми заполнениями внутри каждого регистра. В частности, получено предельное поведение для числа единиц на цикле мультициклической последовательности. В работе [5] проведено исследование устойчивости свойств полученных асимптотических распределений для числа единиц в случае, когда M = 2 и заполнения регистров могут быть зависимы между собой. Свойства мультициклической последовательности при M = 4 и независимых равновероятных знаках в регистрах были исследованы в работе [2]. Получено совместное предельное распределение чисел появлений знаков в мультициклической последовательности, когда длины регистров стремятся к бесконечности.
Настоящая работа посвящена изучению свойств мультициклической последовательности по модулю M = 4 вида длины T, когда случайные векторы 
независимы между собой, но случайные величины 
, образующий j-й вектор, зависимы.
Предельная теорема
Сформулируем 3 условия:
1. Пусть 
, 
независимые в совокупности случайные векторы, компоненты которых имеют равномерное одномерное распределение
2. Пусть при каждом j случайные величины 
m – зависимы по кругу, т.е. наборы случайных величин 
и 
независимы при всех 
.
3. Пусть совместное распределение случайных величин 
инвариантно относительно циклического сдвига, то есть закон распределения набора случайных величин 
при 
совпадает с распределением набора 
где 
.
Определим величины 
равенствами
где 
– число знаков в 
, двоичная запись которых равна 
, 
. Обозначим 
число знаков в 
, имеющих двоичную запись 
. В работе [2] показано, что
(1)
где 
Нас интересует предельный при 
закон распределения случайного вектора 
Ясно, что эта задача эквивалентна задаче о предельном законе распределения случайного вектора 
.
Переходим к изложению основного результата работы. Пусть
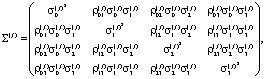
где 
.
Положим
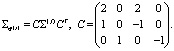
Теорема 11. Пусть выполнены условия 1, 2 и 3, при всех j матрицы 
невырождены. Если параметры m и r фиксированы, а все 
то случайный вектор
сходится по распределению к случайному вектору 
, где
случайные векторы 
независимы между собой и распределены по нормальному закону с нулевыми средними и ковариационными матрицами 
.
Замечание 1. Сравним полученный результат для зависимых заполнений с результатом работы [4]. В ней показано, что при независимых заполнениях регистров 
закон распределения случайного вектора 
сходится к распределению того же вектора 
, но в образующих его наборах 
случайные величина 
и вектор 
независимы между собой. За счет этого удается написать несколько более простое выражение для предельного распределения, основанное на переходе в полярную систему координат.
Замечание 2. Если при всех 
(2)
то ковариационные матрицы 
будут иметь такой же вид, как в теореме 2 работы [2], которая была доказана для случая независимых и равновероятных знаков внутри каждого регистра. При выполнении условий предельный закон распределения из теоремы 1 совпадает с предельным законом, приведенным в теореме 2 работы [2].
Доказательства
Доказательство теоремы 1. Начнем с того, что выпишем первые два момента случайного вектора 
Лемма 11. Пусть выполнены условия 1, 2 и 3. Тогда
(3)
Из формулы следует, что
Рассмотрим вектор
Так как
то 
Следствие 1. Пусть выполнены условия 1, 2 и 3. Тогда случайный вектор 
имеет нулевое среднее и ковариационную матрицу 
Лемма 22. Пусть выполнены условия теоремы 1. Тогда случайный вектор 
асимптотически нормален с нулевым средним и ковариационной матрицей 
Доказательство леммы 1. Сначала выпишем первые два момента величины 
Так как 
то
(4)
(5)
Кроме того, при 
(6)
Формулы следуют из равенств – Лемма 1 доказана.
Доказательство леммы 2. Согласно теореме 1 п. 4 § 13 гл. 2 книги [3] достаточно показать, что любая линейная комбинация 
асимптотически нормальна. Так как вектор 
получен в результате линейного преобразования 
, то вместо случайной величины W можно рассмотреть случайную величину
Сначала вычислим числовые характеристики суммы 
:
(7)
Воспользуемся следующим результатом работы [4]. Пусть 
– система случайных величин с графом зависимостей 
, где множество ребер 
. Граф G строится следующим образом. Каждой случайной величине 
соответствует одна вершина. Если случайные величины зависимы между собой, то их связывает ребро. Если случайные величины независимы, то нет связывающих их ребер. Понятно, что такой граф определен неоднозначно. Если существует такая константа B, что 
для любого 
, то
(8)
где 
, D – максимальная степень вершины в графе G.
Согласно определению
Пусть 
. Положим
Тогда
(9)
Таким образом, к случайной величине 
применима оценка . Граф зависимостей слагаемых суммы имеет множество вершин U. Ясно, что в качестве константы B можно взять 
. Вершины 
и 
, 
, соединены ребрами, если 
. Значит, 
.
Так как 
, то из и получим при 
Таким образом, закон распределения случайной величины 
асимптотически нормален. Лемма 2 доказана.
Из следствия 1, леммы 2, формулы и независимости наборов 
следует утверждение теоремы. Теорема 1 доказана.
Заключение
В работе изучены свойства мультициклической случайной последовательности, образованной независимы между собой регистрами, при этом случайные величины в каждом регистре имеют равновероятные одномерные распределения, но m-зависимы по кругу, а их распределение инвариантно относительно циклического сдвига. Для вектора из чисел появлений знаков {0,1,2,3} на полном цикле мультициклической последовательности доказана многомерная предельная теорема нормального типа в случае, когда длины регистров стремятся к бесконечности, а их число r остается фиксированным. Изучен вопрос об устойчивости соответствующего предельного распределения для случая независимых случайных величин, заполняющих регистры (генератора Пола).
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (тема 1.2640.2014).